
概车伦与散理统外「 第二章 随机变量及其分布 习题课 一、重点与难点 二、主要内容 三、典型例题
一、重点与难点 二、主要内容 三、典型例题 第二章 随机变量及其分布 习 题 课

概率伦与款理统外 一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的分布函数、 密度函数及有关区间概率的计算 2.难点 连续型随机变量的概率密度函数的求法
一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的分布函数、 密度函数及有关区间概率的计算 2.难点 连续型随机变量的概率密度函数的求法
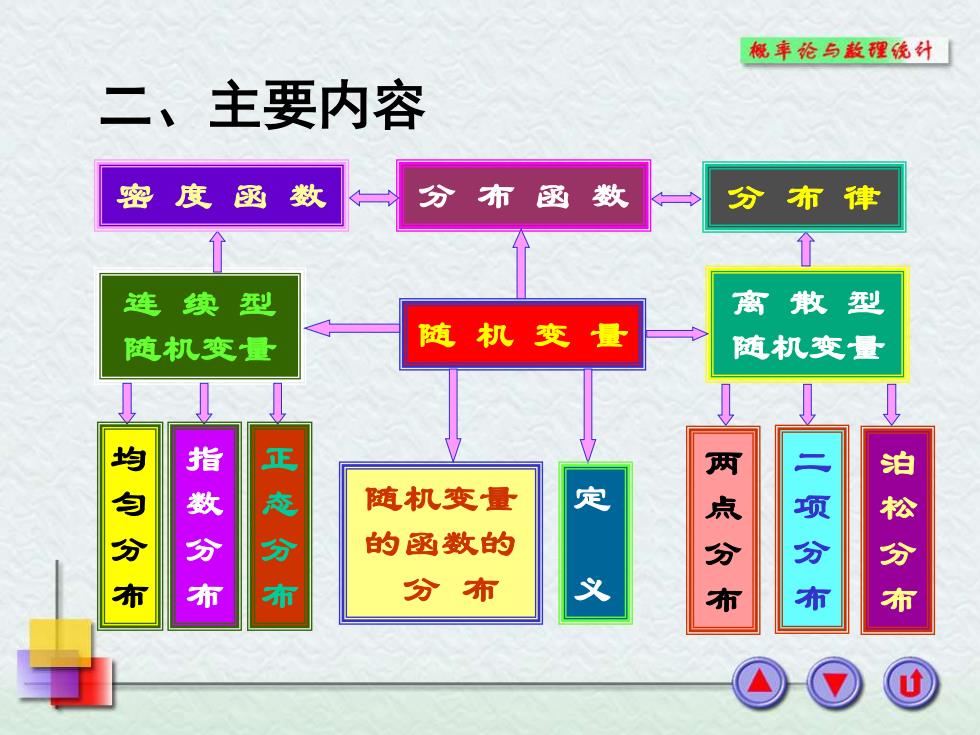
概车纶与款理统外 二、主要内容 密度 函 数 分布函数 布律 连续型 离散型 随机变量 随机变量 随机变量 均匀分布 指教分布 正态分布 随机变量 定 的函数的 分布 义 点分布 项 分 布 松分布
二、主要内容 随 机 变 量 离 散 型 随机变量 连 续 型 随机变量 密 度 函 数 分 布 函 数 分 布 律 均 匀 分 布 指 数 分 布 正 态 分 布 两 点 分 布 二 项 分 布 泊 松 分 布 随机变量 的函数的 分 布 定 义

概率伦与款理统外 随机变量 定义设E是随机试验,它的样本空间是S={.如 果对于每一个e∈S,有一个实数X(e)与之对应,这 样就得到一个定义在S上的单值实值函数X(e),称 随机变量 (1)随机变量与普通的函数不同 随机变量是一个函数,但它与普通的函数有着 本质的差别,普通函数是定义在实数轴上的,而随机 变量是定义在样本空间上的(样本空间的元素不一 定是实数)
随机变量是一个函数 ,但它与普通的函数有着 本质的差别 ,普通函数是定义在实数轴上的,而随机 变量是定义在样本空间上的 (样本空间的元素不一 定是实数). . ( ), , ( ) , , { }. 随机变量 样就得到一个定义在 上的单值实值函数 称 果对于每一个 有一个实数 与之对应 这 定义 设 是随机试验 它的样本空间是 如 S X e e S X e E S e = (1)随机变量与普通的函数不同 随机变量

概车纶与散理统针「 (2)随机变量的取值具有一定的概率规律 随机变量随着试验的结果不同而取不同的值, 由于试验的各个结果的出现具有一定的概率,因此 随机变量的取值也有一定的概率规律. (3)随机变量与随机事件的关系 随机事件包容在随机变量这个范围更广的概 念之内或者说:随机事件是从静态的观点来研究 随机现象,而随机变量则是从动态的观点来研究随 机现象
随机变量随着试验的结果不同而取不同的值, 由于试验的各个结果的出现具有一定的概率,因此 随机变量的取值也有一定的概率规律. (2)随机变量的取值具有一定的概率规律 (3)随机变量与随机事件的关系 随机事件包容在随机变量这个范围更广的概 念之内.或者说 : 随机事件是从静态的观点来研究 随机现象,而随机变量则是从动态的观点来研究随 机现象