
儿个橇念: 可行解:满足线性规划所有约束条件(含约束方程与变量 约束)的点。 可行解域:所在可行解的集合。 心最优解:使目标函数得到极值的可行解。最优解包括:唯 一最优解和无穷多最优解。 等值线:具有相同目标函数值的直线。 法向量(梯度):由目标函数系数组成的与等值线垂直的向 量
21 几个概念: ❖可行解:满足线性规划所有约束条件(含约束方程与变量 约束)的点。 ❖可行解域:所在可行解的集合。 ❖最优解:使目标函数得到极值的可行解。最优解包括:唯 一最优解和无穷多最优解。 ❖等值线:具有相同目标函数值的直线。 ❖法向量(梯度):由目标函数系数组成的与等值线垂直的向 量

二、二维线性规划问题解的形式 1、唯一最优解 X2 2、无穷多个最优解 Max Z=x+2x2 x+比2≤6 X+2x2≤8 可行解域 t2≤3 2,3 x≥0=1,2) Q2(4,2) 目标函数的等值线 22
22 二、二维线性规划问题解的形式 1、唯一最优解 2、无穷多个最优解 6 6 8 4 3 x2 可行解域 目标函数的等值线 C(1,2) Q2 (4,2) Q3 (2,3) x1 Max Z=x1+2x2 x1+x2≤6 x1+2x2≤8 x2≤3 xi≥0(i=1,2)
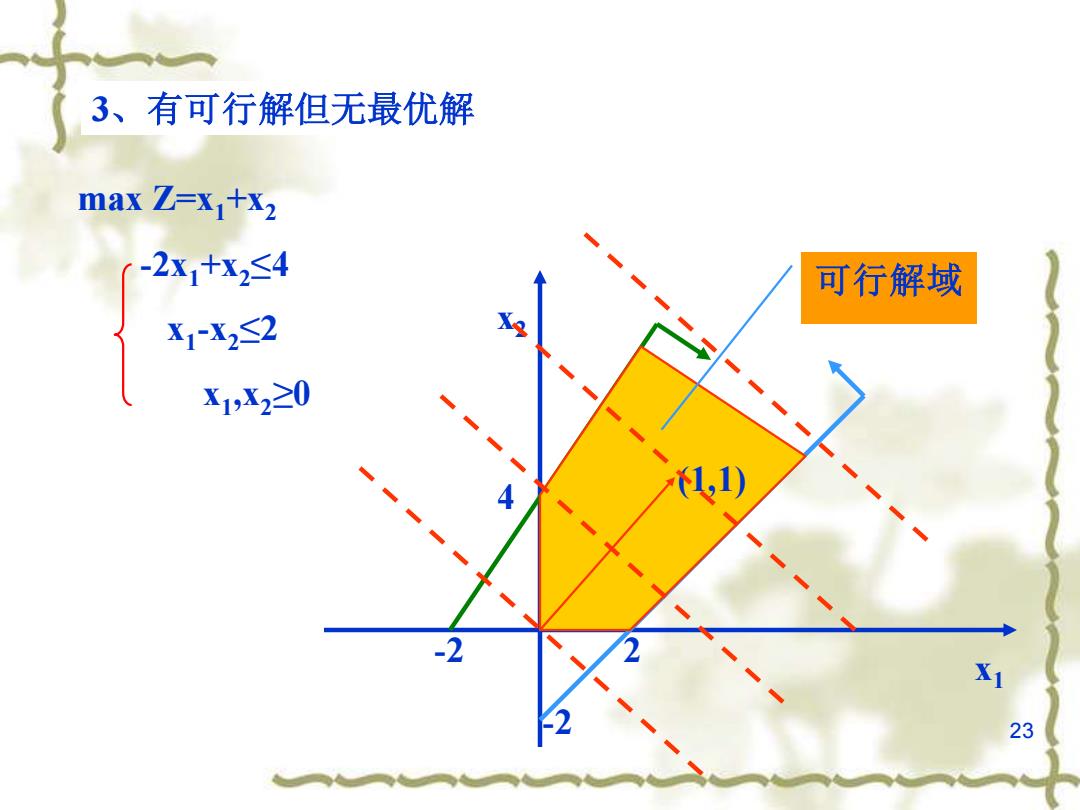
3、有可行解但无最优解 max Z=x+X2 -2x+X2≤4 可行解域 X1X2≤2 X1,X2≥0 ,0) 2 23
23 3、有可行解但无最优解 max Z=x1+x2 -2x1+x2 ≤4 x1 -x2 ≤2 x1 ,x2 ≥0 x2 x1 -2 4 -2 2 可行解域 (1,1)
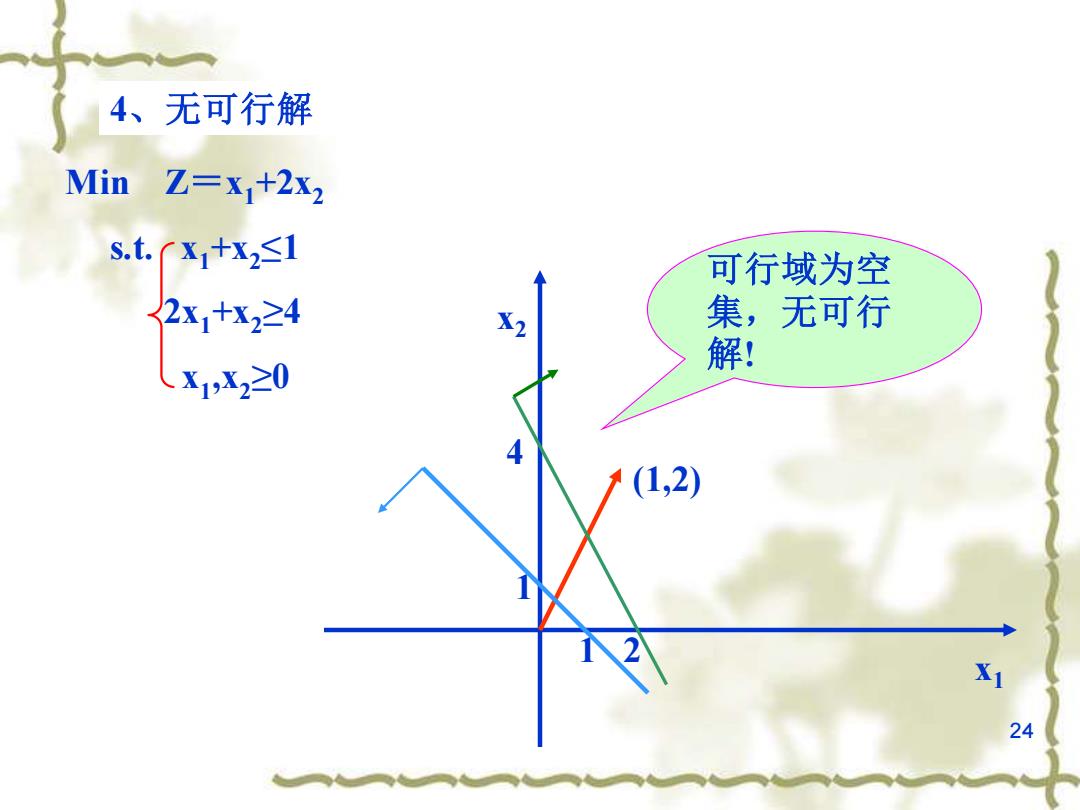
4、无可行解 Min Z=x+2x2 s.t.x1+x2≤1 可行域为空 2x+x224 集,无可行 X1,X2≥0 解! (1,2) 24
24 4、无可行解 Min Z=x1+2x2 s.t. x1+x2 ≤1 2x1+x2 ≥4 x1 ,x2 ≥0 x2 x1 1 1 4 2 (1,2) 可行域为空 集,无可行 解!
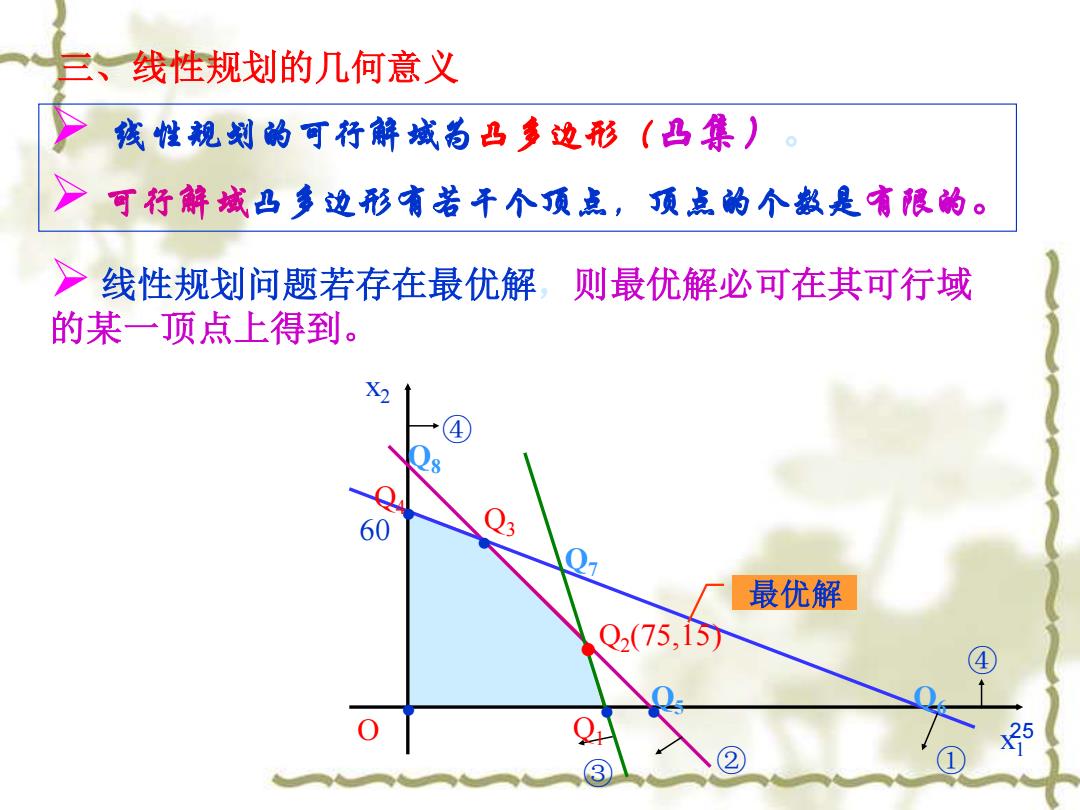
三、线性规划的几何意义 线性规划的可行解域为凸多边形(凸集) 可行解域凸多边形有若干个顶点,顶点的个数是有限的。 >线性规划问题若存在最优解 ,则最优解必可在其可行域 的某一顶点上得到。 最优解 Q2(75,15 ③
25 ➢ 线性规划的可行解域为凸多边形(凸集)。 ➢ 可行解域凸多边形有若干个顶点,顶点的个数是有限的。 三、线性规划的几何意义 ➢ 线性规划问题若存在最优解,则最优解必可在其可行域 的某一顶点上得到。 • • • • • O x1 x2 Q2 (75,15) 60 ③ ② ④ ④ ① • 最优解 Q1 Q3 Q4 Q5 Q6 Q7 Q8