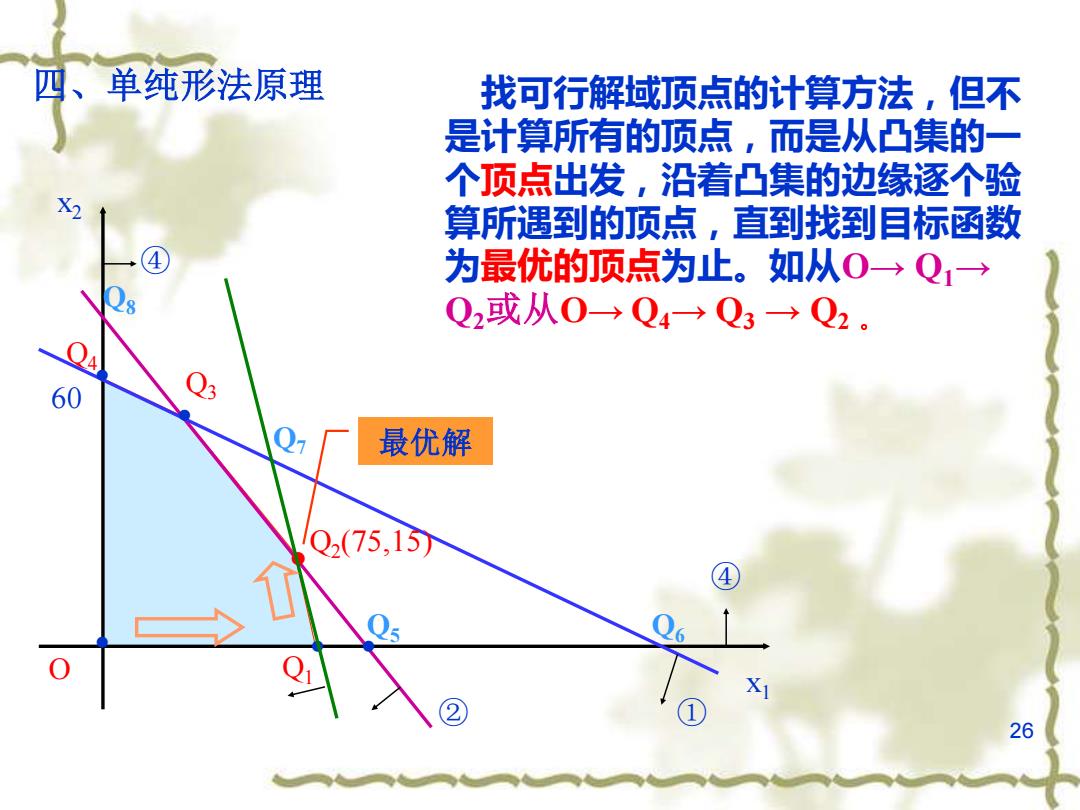
四、单纯形法原理 找可行解域顶点的计算方法,但不 是计算所有的顶点,而是从凸集的一 个顶点出发,沿着凸集的边缘逐个验 X 算所遇到的顶点,直到找到目标函数 为最优的顶点为止。如从O→Q1→ Q2或从0→Q4→Q3→Q2。 60 最优解 Q2(75,15) 26
26 四、单纯形法原理 • • • • • O x1 x2 Q2 (75,15) 60 ② ④ ④ ① • 最优解 Q1 Q3 Q4 Q5 Q6 Q7 Q8 找可行解域顶点的计算方法,但不 是计算所有的顶点,而是从凸集的一 个顶点出发,沿着凸集的边缘逐个验 算所遇到的顶点,直到找到目标函数 为最优的顶点为止。如从O→ Q1→ Q2或从O→ Q4→ Q3 → Q2

§5.3 孩性规划标准型和规范型 线性规划的标准型 ①约束方程均为等式方程。 ②右边常数b为正数。 max Z=Cx+Cx+.+Cxm ③所有变量均为非负变量。 ④目标函数求max ax+a2x2+...+ainxn =b a2+a22x2+.+anx=b2 1、一般形式: am +am2X2++amnn=bm X1,X2,…,Xn≥0 27
27 §§1.35.3 单纯形法原理 线性规划标准型和规范型 一、线性规划的标准型 ①约束方程均为等式方程。 ②右边常数bi为正数。 ③所有变量均为非负变量。 ④目标函数求max 1、一般形式: 1 1 2 2 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 1 2 max , , , 0 n n n n n n m m mn n m n Z c x c x c x a x a x a x b a x a x a x b a x a x a x b x x x = + + + + + + = + + + = + + + =

或写成累加和形式: maxZ=∑c,x =1 2a,=4i=1m = max Z=Cx+Cx++Cnxn xj≥0, j=1,…n a1x1+a2x2+…+anXn=b a2+a22x2+..+ann=b2 amx+am2x2++amxn =bm 标准型的一般形式 X1,X2,…,Xn≥0 28
28 = = = = = = x j n a x b i m Z c x j n j ij j i n j j j 0, 1, , 1, max 1 1 或写成累加和形式: 1 1 2 2 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 1 2 max , , , 0 n n n n n n m m mn n m n Z c x c x c x a x a x a x b a x a x a x b a x a x a x b x x x = + + + + + + = + + + = + + + = 标准型的一般形式

或写成矩阵形式: max Z=c+cx2++cx maxZ=CX ax+a2x2+...+aunxn=b a2x+a22x2+..+anxn=b AX=b X≥0 am+am22+amn=bm 其中: 1,X2,…,xn≥0 d11 2 A= a21 02 X= X2 b, b= P,= tz am b」 C=(C,C2,…Cn) 则A=[,P2,…Pn] 29
29 max 0 Z CX AX b X = = 或写成矩阵形式: 1 1 2 2 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 1 2 max , , , 0 n n n n n n m m mn n m n Z c x c x c x a x a x a x b a x a x a x b a x a x a x b x x x = + + + + + + = + + + = + + + = 11 12 1 21 22 2 1 2 , n n m m mn a a a a a a A a a a = 1 2 , n x x X x = 1 2 , n b b b b = 1 2 ( , , ) C c c c = n 1 2 j j j mj a a P a = 其中: 1 2 [ , , ] 则A P P P = n

2、化线性规划问题为标准型 (1)约束条件为等式 ①约束方程为“≤“号, 在方程式的左端“十”一个变量(变量≥0,称为松驰变 量),原不等式化为等式约束。 ②约方程为“≥”号 在方程式的左端“一”一个变量(变量≥0,称为剩余变 量),原不等式化为等式约束。 30
30 2、化线性规划问题为标准型 ①约束方程为“≤“号, 在方程式的左端“+”一个变量(变量≥0,称为松驰变 量),原不等式化为等式约束。 ②约束方程为“≥”号 在方程式的左端“-”一个变量(变量≥0,称为剩余变 量),原不等式化为等式约束。 (1) 约束条件为等式