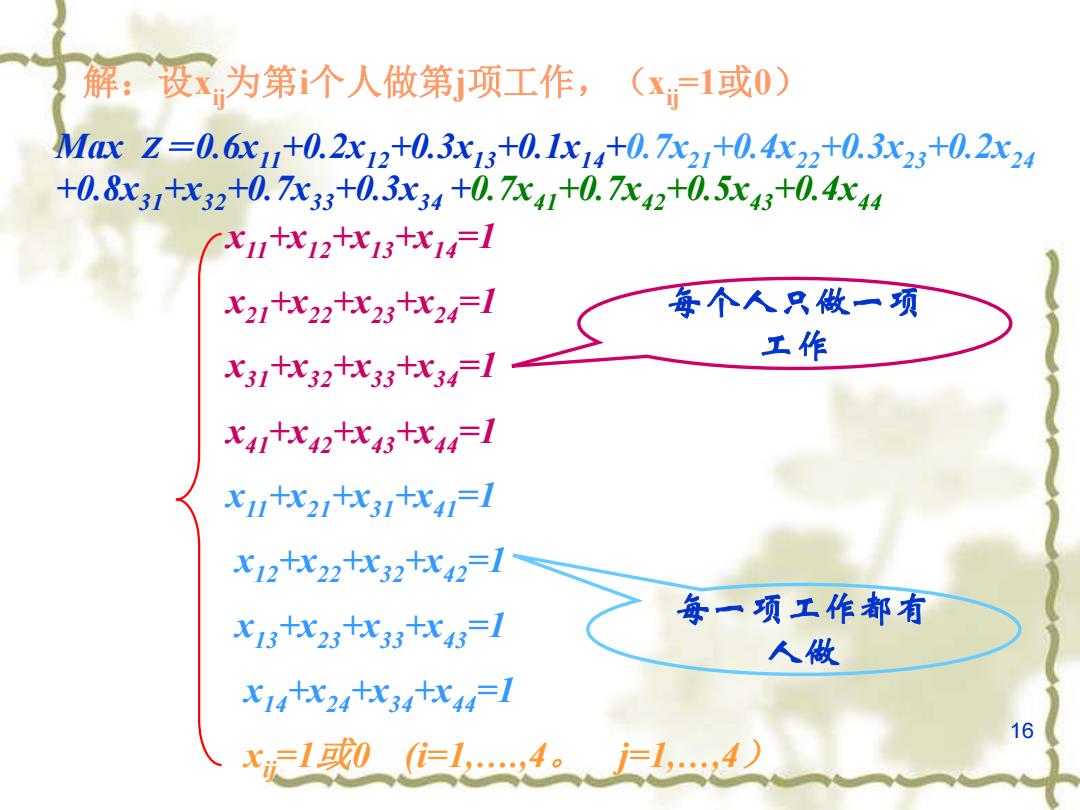
解:设x为第个人做第项工作,(x1或0) MacZ=0.6c+0.2x12+0.3x3+0.1x14+0.7x2+0.4x22t0.3x23+0.2x24 +0.8x3t比32十0.7x33+0.3x34+0.7x4+0.7x42t0.5x43十0.444 x1t比12t比13t比1Fl x21tx22t比23t比24Fl 每个人只做一项 工作 七31tx32t比3tx3l x41t比42tx43tx44Fl X1比21t比31比41l X12t22t比32t比42l X13t比23t比33比l 每一项工作都有 人做 x14t比24t比34t比44Fl 16 x1或0=,4。广,4)
16 解:设xij为第i个人做第j项工作,(xij =1或0) Max Z=0.6x11+0.2x12+0.3x13+0.1x14+0.7x21+0.4x22+0.3x23+0.2x24 +0.8x31+x32+0.7x33+0.3x34 +0.7x41+0.7x42+0.5x43+0.4x44 x11+x12+x13+x14 =1 x21+x22+x23+x24 =1 x31+x32+x33+x34 =1 x41+x42+x43+x44 =1 x11+x21+x31+x41 =1 x12+x22+x32+x42 =1 x13+x23+x33+x43 =1 x14+x24+x34+x44 =1 xij =1或0 (i=1,….,4。 j=1,…,4) 每一项工作都有 人做 每个人只做一项 工作

线性规划建模小结 线性规划的共同点: 要解决的问题的目标可以用数值指标反映 对于要实现的目标有多种方案可选择 有影响决策的若干约束条件 线性规划建立模型步骤: 确定一组决策变量 确定目标函数 确定对决策变量的约束条件 17
17 ❖线性规划建立模型步骤: ▪ 确定一组决策变量 ▪ 确定目标函数 ▪ 确定对决策变量的约束条件 线性规划建模小结 ❖线性规划的共同点: ▪ 要解决的问题的目标可以用数值指标反映 ▪ 对于要实现的目标有多种方案可选择 ▪ 有影响决策的若干约束条件
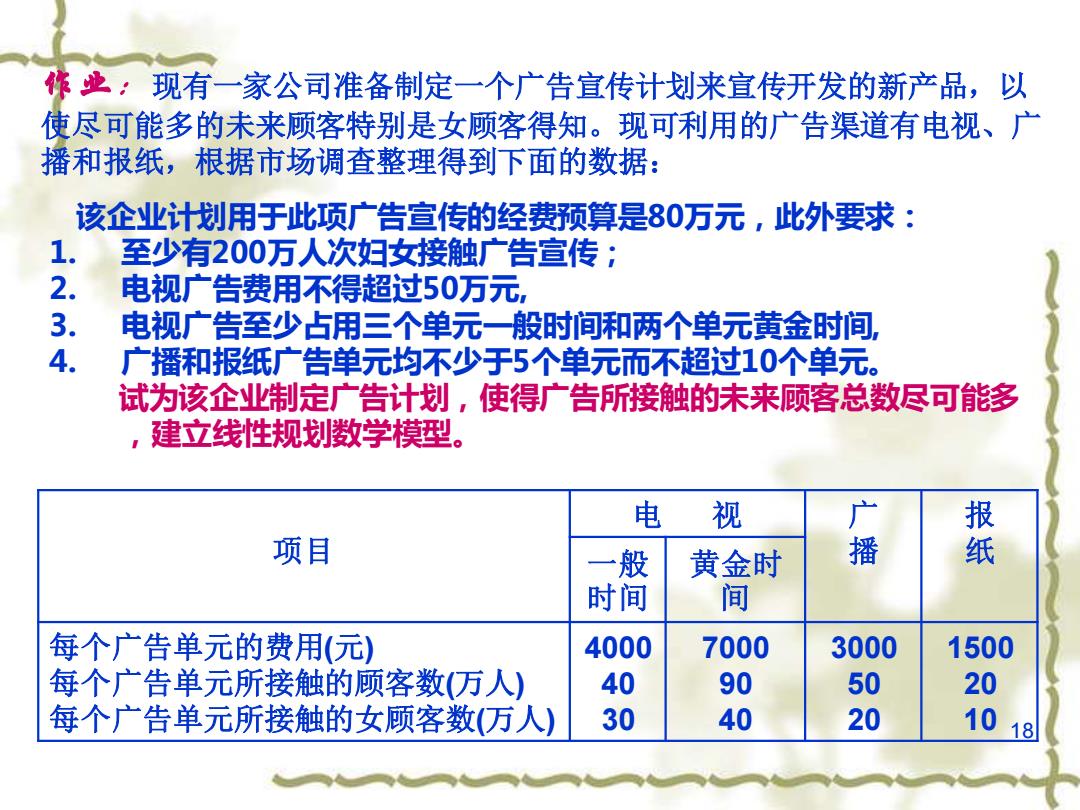
修业:现有一家公司准备制定一个广告宣传计划来宣传开发的新产品,以 使尽可能多的未来顾客特别是女顾客得知。现可利用的广告渠道有电视、广 播和报纸,根据市场调查整理得到下面的数据: 该企业计划用于此项广告宣传的经费预算是80万元,此外要求: 1. 至少有200万人次妇女接触广告宣传; 2. 电视广告费用不得超过50万元, 电视广告至少占用三个单元一般时间和两个单元黄金时间, 4. 广播和报纸广告单元均不少于5个单元而不超过10个单元。 试为该企业制定广告计划,使得广告所接触的未来顾客总数尽可能多 建立线性规划数学模型。 电视 广 项目 一般 黄金时 播 纸 时间 间 每个广告单元的费用(元) 4000 7000 3000 1500 每个广告单元所接触的顾客数(万人) 40 90 50 2 每个广告单元所接触的女顾客数(万人) 30 40 20 10 18
18 作业:现有一家公司准备制定一个广告宣传计划来宣传开发的新产品,以 使尽可能多的未来顾客特别是女顾客得知。现可利用的广告渠道有电视、广 播和报纸,根据市场调查整理得到下面的数据: 项目 电 视 广 播 报 一般 纸 时间 黄金时 间 每个广告单元的费用(元) 每个广告单元所接触的顾客数(万人) 每个广告单元所接触的女顾客数(万人) 4000 40 30 7000 90 40 3000 50 20 1500 20 10 该企业计划用于此项广告宣传的经费预算是80万元,此外要求: 1. 至少有200万人次妇女接触广告宣传; 2. 电视广告费用不得超过50万元, 3. 电视广告至少占用三个单元一般时间和两个单元黄金时间, 4. 广播和报纸广告单元均不少于5个单元而不超过10个单元。 试为该企业制定广告计划,使得广告所接触的未来顾客总数尽可能多 ,建立线性规划数学模型

§5,2 线性规划的图解法 图解法求最优解的步骤 对于简单的线性规划问题(只有两个决策变量的线性规划 问题),我们通过图解法可以对它进行求解。 思路:在直角坐标系中,描绘出约束条件和变量限制的公 共区域,然后通过观察确定符合目标要求的变量的取值。 求解例1中的生产计划问题: 19
19 §5.2 线性规划的图解法 一、图解法求最优解的步骤 思路:在直角坐标系中,描绘出约束条件和变量限制的公 共区域,然后通过观察确定符合目标要求的变量的取值。 求解例1中的生产计划问题: 对于简单的线性规划问题(只有两个决策变量的线性规划 问题),我们通过图解法可以对它进行求解
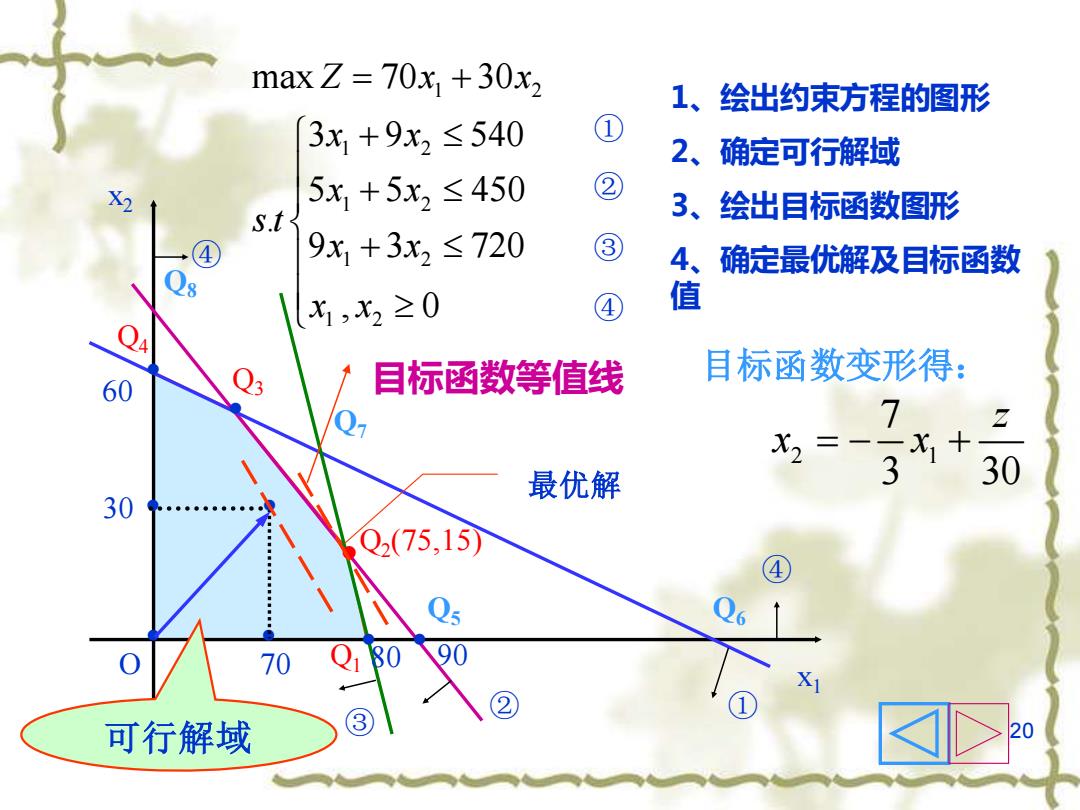
max Z=70x+30x, 1、绘出约束方程的图形 3x,+9x2≤540 ① 2、确定可行解域 X 5x,+5x2≤450 ② s.t3 3、绘出目标函数图形 9x1+3x2≤720 ③ 4、 确定最优解及目标函数 x1,X2≥0 值 4 目标函数变形得: 60 目标函数等值线 7 X2=-5X1+ 最优解 3 30 30 Q2(75,15) 70 可行解域
20 ② ③ ① ④ 1 2 1 2 1 2 1 2 1 2 max 70 30 3 9 540 5 5 450 . 9 3 720 , 0 Z x x x x x x s t x x x x = + + + + • • • • • O x1 x2 80 60 30 70 • • • ② ③ ④ ④ ① 90 • 1、绘出约束方程的图形 2、确定可行解域 3、绘出目标函数图形 4、确定最优解及目标函数 值 可行解域 目标函数变形得: 2 1 7 3 30 z x x = − + 目标函数等值线 最优解 Q2 (75,15) Q1 Q3 Q4 Q5 Q6 Q7 Q8