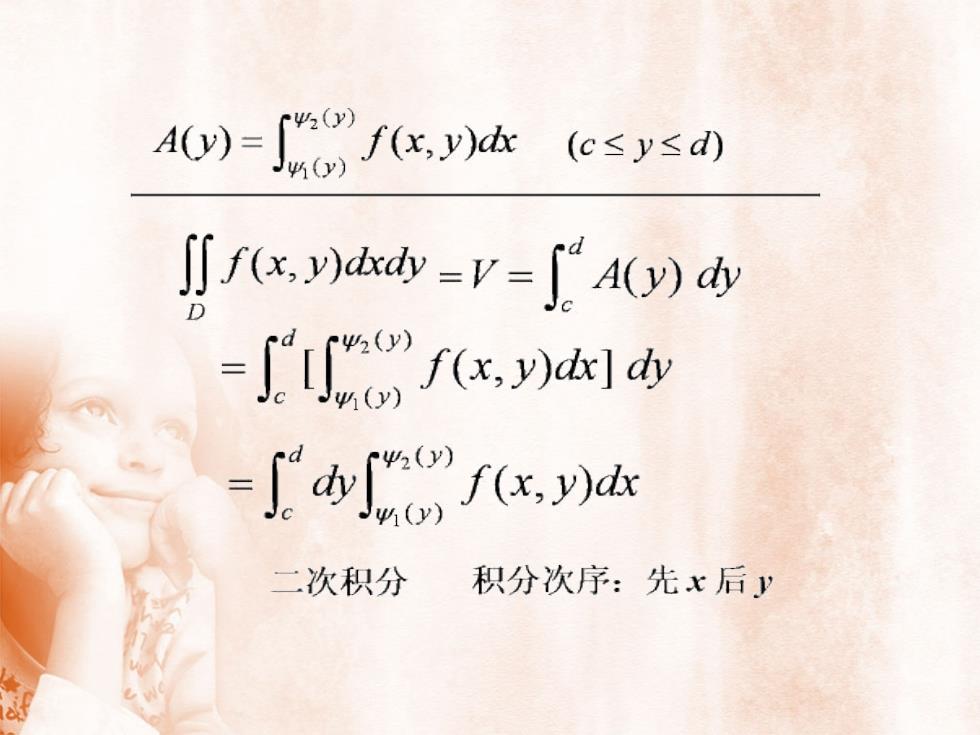
2)A() =f(x, y)dx(c≤y≤d)J)J f(x, y)dxdy =V= [" A(y) dyDT'tof(x, y)dx) dyV42(y)dyf(x, y)dxwi(y)二次积分积分次序:先x后J
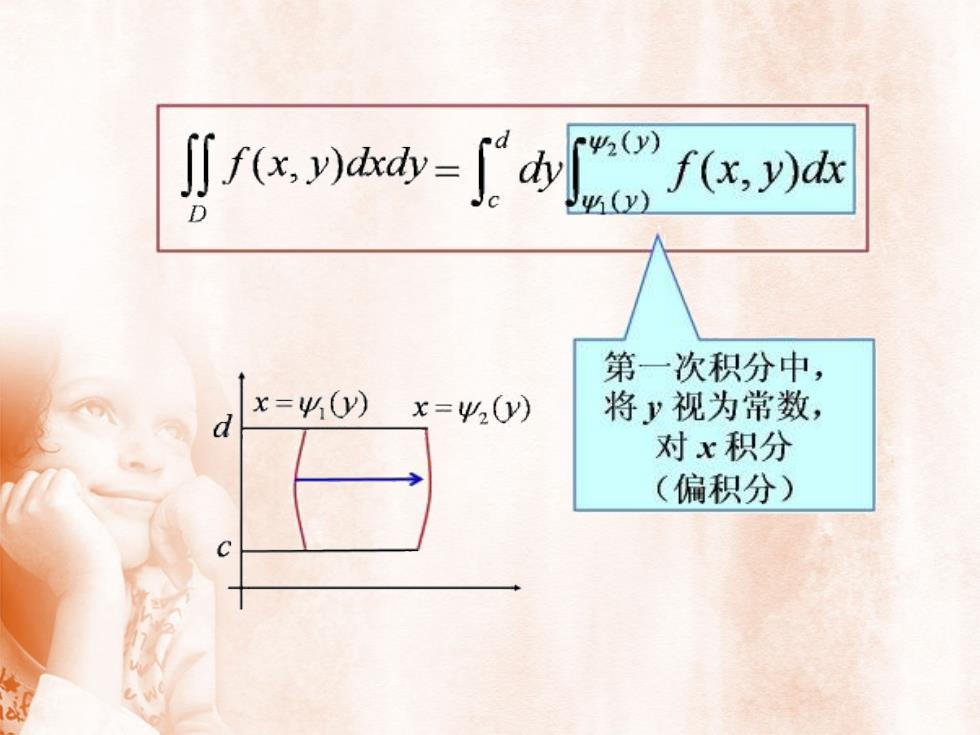
W2(y)J f(x, y)dxdy =f(x,y)dxy(y)D第一次积分中,x=y)将视为常数,x=W,(y)d对x积分(偏积分)C

矩形区域上的二重积分矩形区域DD=(x y)la<≤x<b c≤y≤d)bJJ f(x, y)ady ="'dx"f(x,ydy先y后xDf f(x, y)dxdy = ["dy" f(x, yldx先x后yD

特别地,如果CIf(x, y) = h(x)g(y)bJ h(x)g(y)dxdy = f' h(x)dx f" g(y)dyD即分别计算两个定积分,再相乘
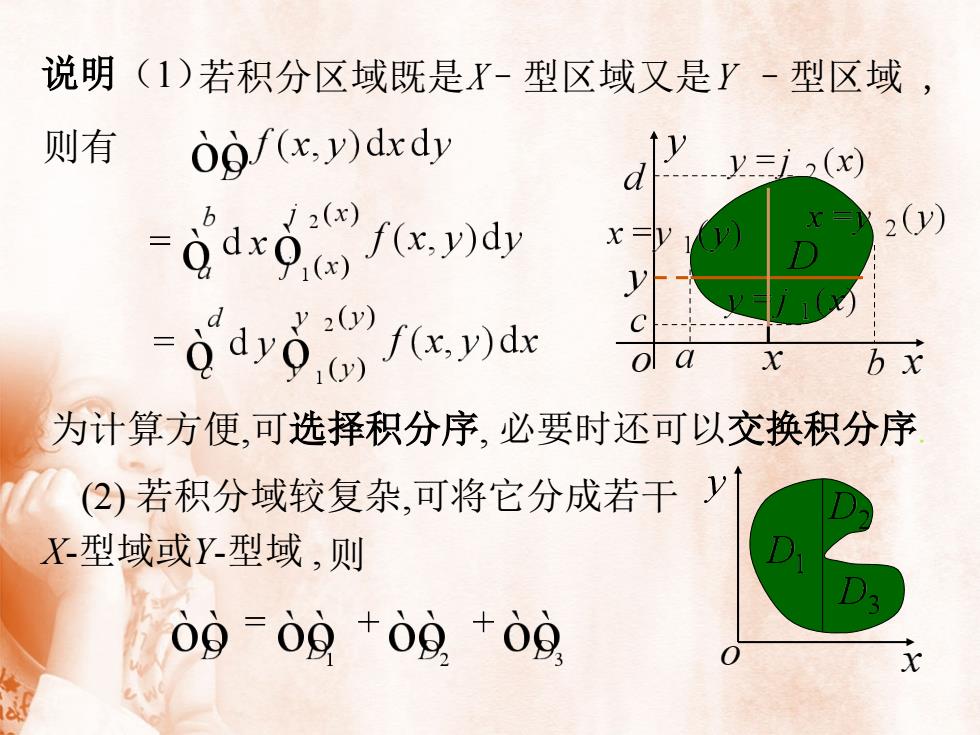
说明(1)若积分区域既是X-型区域又是Y-型区域,则有yogf(x,y)dxdyy=j 2(x)d/ 2(x)2(y)h=dx9f(x,y)dyx=VDy2c0'dyg) f(x,y)dxxolabx1为计算方便,可选择积分序,必要时还可以交换积分序(2)若积分域较复杂,可将它分成若干 DX-型域或Y-型域,则D309=09 +0g +09Ox
若积分区域既是X–型区域又是Y –型区域 , 为计算方便,可选择积分序, 必要时还可以交换积分序. 则有 (2) 若积分域较复杂,可将它分成若干 X-型域或Y-型域 , 则 说明(1)