
第十章重积分在一元函数积分学中,我们已经知道,定积分是定义在某一区间上的一元函数的某种特定形式的和式的极限,由于科学技术和生产实践的发展,需要计算空间形体的体积、曲面的面积、空间物体的质量、重心、转动惯量等,定积分已经不能解决这类问题,另一方面,从数学逻辑思维的规律出发,必然会考虑定积分概念的推广,从而提出了多元函数的积分学问题
第十章 重 积 分 在一元函数积分学中,我们已经知道,定积 分是定义在某一区间上的一元函数的某种特定形 式的和式的极限,由于科学技术和生产实践的发 展,需要计算空间形体的体积、曲面的面积、空 间物体的质量、重心、转动惯量等,定积分已经 不能解决这类问题,另一方面,从数学逻辑思维 的规律出发,必然会考虑定积分概念的推广,从 而提出了多元函数的积分学问题

“大当人们把定积分解决问题的基本思想化小、常代变、近似和、求极限”用于解决这类问题时发现是完全可行的。把解决的基本方法抽象概括出来,就得到多元函数积分学。具体地说就是推广到:定义在平面区域上的二元函数、定义在空间区域上的三元函数、定义在一段平面曲线弧上的二元函数、定义在空间一段曲线弧上的三元函数、定义在空间曲面上的三元函数,从而得到二重积分、三重积分、曲线积分和曲面积分。这就是多元函数积分学的内容。本章将讨论重积分,包括二重积分、三重积分的概念、性质、计算和应用
当人们把定积分解决问题的基本思想——“大 化小、常代变、近似和、求极限”用于解决这类 问题时发现是完全可行的。把解决的基本方法抽 象概括出来,就得到多元函数积分学。 具体地说就是推广到:定义在平面区域上的二元 函数、定义在空间区域上的三元函数、定义在一段 平面曲线弧上的二元函数、定义在空间一段曲线弧 上的三元函数、定义在空间曲面上的三元函数,从 而得到二重积分、三重积分、曲线积分和曲面积分。 这就是多元函数积分学的内容。 本章将讨论重积分,包括二重积分、三重积分 的概念、性质、计算和应用

第一节二重积分的概念与性质一、引例二、 二重积分的定义与可积性三、 二重积分的性质
三、二重积分的性质 第一节 一、引例 二、二重积分的定义与可积性 二重积分的概念与性质

回忆:曲边梯形的面积的求法y=f(x)AXXbXa-axx5A-ZA~Zf(5)AxA~f(E)Ax三i=l
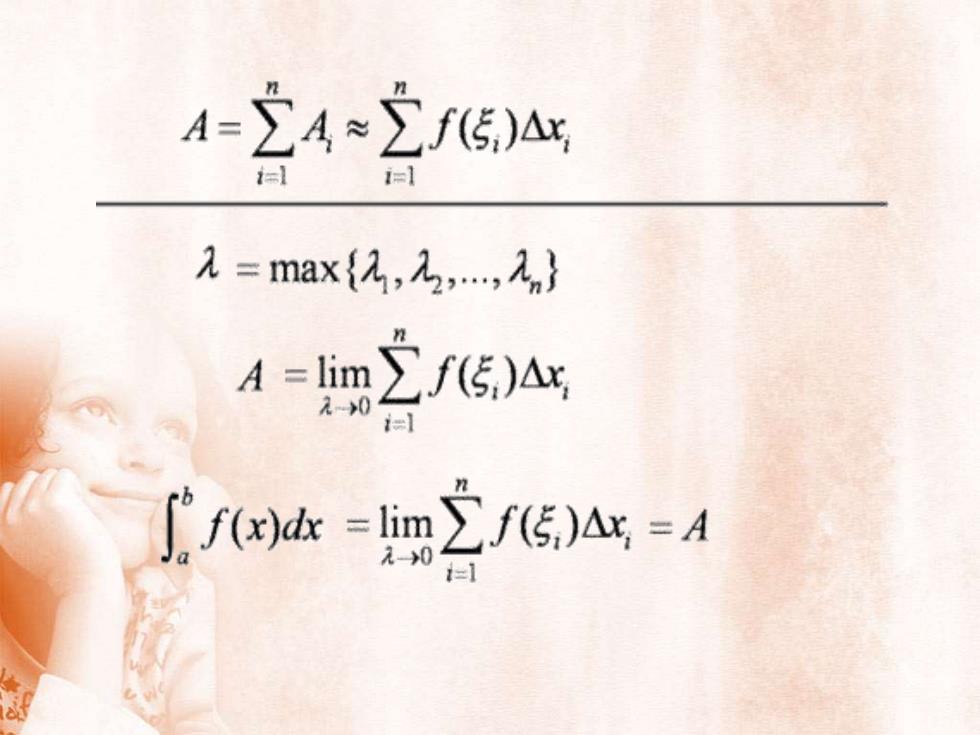
A-ZA ~Zf(5)Ax,tli=l1 =max(a,2..,,nZf(5)Ax,A=lim元→0三lnZf(5)A =A=limf(x)dx元-→0t=1