《线性代数》课程教学课件（PPT讲稿，C）矩阵的运算

定义若A=(a)x,B=(bg)xn, 规定AB=C=(c)mxn, 其中c=a,+a4,++a.b之ab (i=1,2,.,m;j=1,2,.,D 注：1)条件左矩阵A的列数等于右矩阵B的行数 2)结果左行右列一左矩阵A的行数为乘积 C的行数，右矩阵B的列数为乘积C的列数

2、定义 ( ) , AB C c = = ij m n ( ) ( ) , 若 A a B b = = ij m n   s s ， ij 规定 1 1 2 2 1 ij i j i j is sj ik kj c a b a b a b a b = = + + +  ｓ ｋ 其中 ＝ （i m j n = = 1 2 1 2 ， ，； ， ，） 注： 1）条件 左矩阵Ａ的列数等于右矩阵Ｂ的行数 2）结果 左行右列——左矩阵Ａ的行数为乘积 Ｃ的行数，右矩阵Ｂ的列数为乘积Ｃ的列数

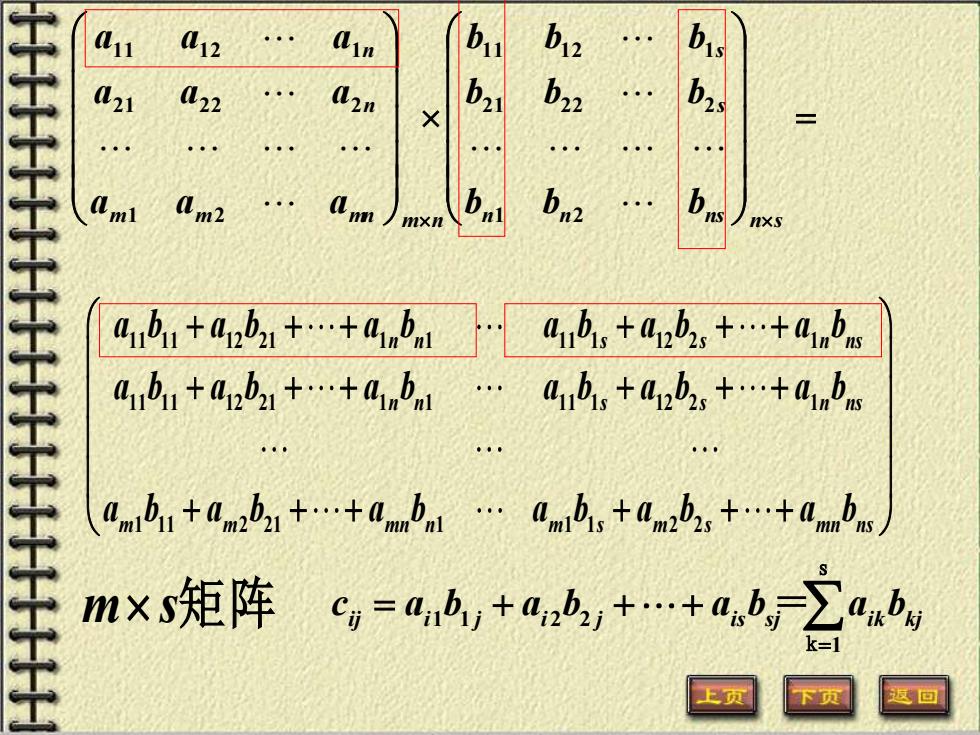
L11 12 b12 21 422 b21 D22 Am2 mxn b心 4b,+0zb1+.+anb a,+0b2,+.+ab ab1+a,b1++4bnl. 4nb,+a2b,++4b amuaamaamisasms m×S矩阵cg=ab,+a,h,++ab,-∑abg 上页

m m mn m n n n a a a a a a a a a                       1 2 2 1 2 2 2 1 1 1 2 1 =                n n ns ns s s b b b b b b b b b        1 2 2 1 2 2 2 1 1 1 2 1 11 11 12 21 1 1 11 1 12 2 1 11 11 12 21 1 1 11 1 12 2 1 1 11 2 21 1 1 1 2 2 n n s s n ns n n s s n ns m m mn n m s m s mn ns a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b   + + + + + +   + + + + + +       + + + + + +   m s矩阵 = = + + + 1 1 2 2  1 ij i j i j is sj ik kj c a b a b a b a b ｓ ｋ ＝

例1 2×2 例2 设 0 3 (1 -1 2 2 A= 1 3 0 B- 1 3 1 0 5 -1 4 _1 2 回

例１ 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = −16 − 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ?

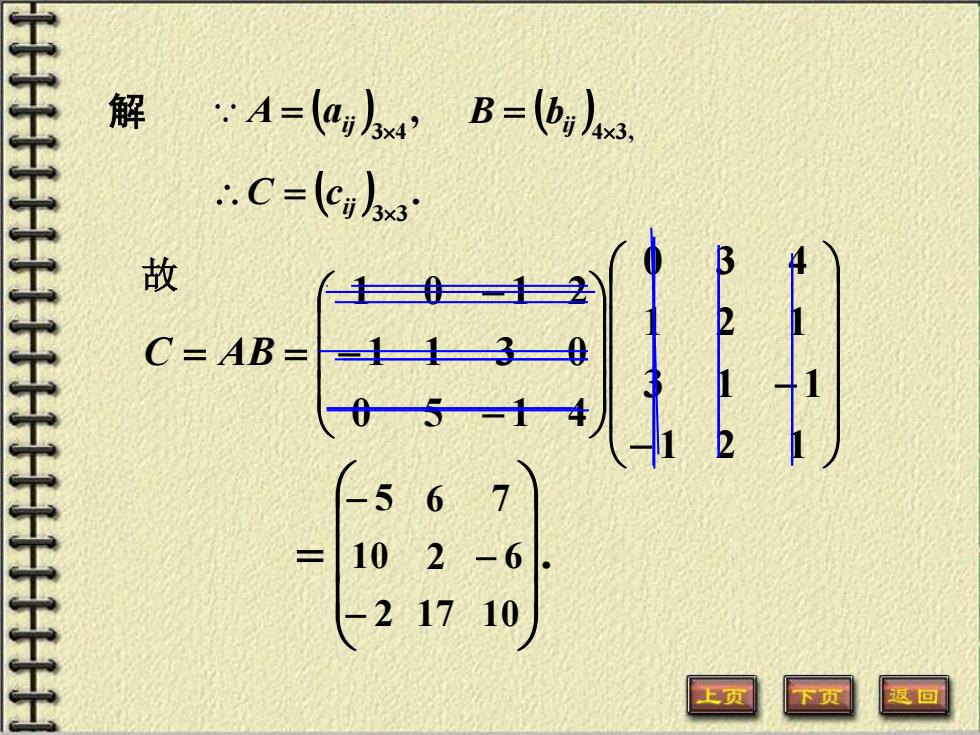
解 A=agA4’B=bg .C=(ei 故 C=AB= 05-十4 5 6 10 2 -6 217 10

故   − −   − − − = = 1 2 1 3 1 1 1 2 1 0 3 4 0 5 1 4 1 1 3 0 1 0 1 2 C AB .  = 解 ( ) , 34  A = aij ( )4  3 , B = bij ( ) . 33  = ij C c − 5 6 7 10 2 − 6 − 2 17 10