《线性代数》课程教学课件（PPT讲稿，C）矩阵的运算

第二草矩阵的运算 九小结 七六五四三二 一 乘数 伴随麵阵 方阵的行到式 短阵的转置 耗阵的羅 法乘 上页 下页

课前复习 1、矩阵的定义 由数域F中的m×n个数排成的m行n列的矩 形数表，称为数域F中的一个m×n矩阵. 12 记作：A= 21 22 021 mn 注：行矩阵，列矩阵，方阵，方阵的行列式，两矩 阵同型，两矩阵相等：

课前复习 1、矩阵的定义 形数表，称为数域Ｆ中的一个ｍ×ｎ矩阵. 由数域Ｆ中的ｍ×ｎ个数 排成的ｍ行ｎ列的矩 ij a 记作： 11 12 1 21 22 2 1 1 n n m m mn a a a a a a A a a a     =         注：行矩阵，列矩阵，方阵，方阵的行列式，两矩 阵同型，两矩阵相等

方阵(m=n方 2、特殊矩阵 行矩阵与列矩阵；A= n) 单位矩阵； 西 对角矩阵； 零矩阵。 回

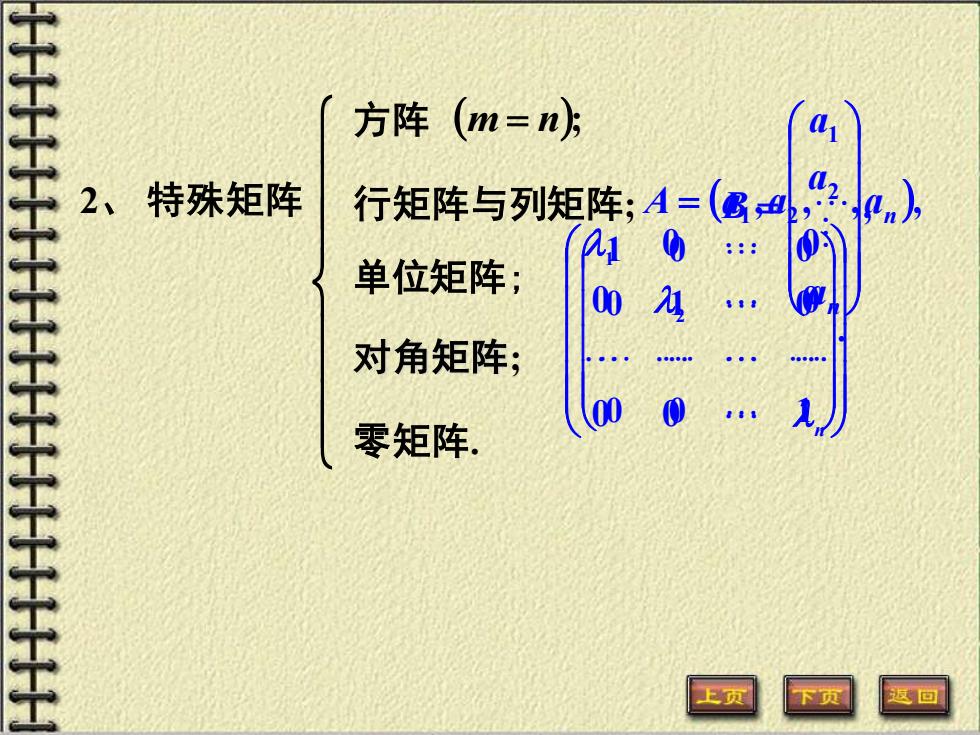
2、 特殊矩阵        方阵 (m = n); 行矩阵与列矩阵; 单位矩阵; 对角矩阵; 零矩阵. . 0 0 1 0 1 0 1 0 0                      , 2 1               = an a a B  ( , , , ), 1 2 n A = a a  a                n          0 0 0 0 0 0 2 1

3.1.1、矩阵的加法 1、定义 设有两个m×n矩阵A=(a,人B=(b,)那末矩阵 A与B的和记作A+B,规定为 4u+b1 a2+b2 az +ba ax+b22 4+B=

１、定义               + + + + + + + + + + = m m m m m n m n n n n n a b a b a b a b a b a b a b a b a b A B        1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 3.1.1 、矩阵的加法 设有两个 矩阵 那末矩阵 与 的和记作 ，规定为 mn A (a ), B (b ), = ij = ij A B A+ B

说明只有当两个矩阵是同型矩阵时，才能进 行加法运算. 12 3 -5 18 9 例如 1 -9 0 + 6 5 4 3 6 8 3 21 12+1 3+8 -5+9 13 11 1+6 -9+5 0+4 -4 3+3 6+2 8+1 8 上页 回

说明 只有当两个矩阵是同型矩阵时，才能进 行加法运算. 例如           +           − − 3 2 1 6 5 4 1 8 9 3 6 8 1 9 0 12 3 5           + + + + − + + + + − + = 3 3 6 2 8 1 1 6 9 5 0 4 12 1 3 8 5 9 . 6 8 9 7 4 4 13 11 4           = −