《线性代数》课程教学课件（PPT讲稿，C）向量的线性相关性

三向量的线性相性 线性组合 方程组、矩阵、向量组的关系 二 三 向量组的线性相关性 四、向量组的秩 五向量空间的维数 上页 返回

四、向量组的秩 一 线性组合 三 向量组的线性相关性 五 向量空间的维数 二 方程组、 矩 阵 、 向量组的关系

课前复习 一、向量的线性相关性 定义2.3.1设向量组A:a41,a2,am和向量B, 如果存在一组数1，入2，入m使 B=入，C1+2x2+.+入mAm 则向量B是向量组A:%1,a2,.的m一个线性组合， 或称向量B可由向量组A线性表示

一、向量的线性相关性 定义2.3.1设向量组 A:1 ,2 ,  , m 和向量，        = + + 1 1 2 2 m m + 如果存在一组数1 ，2 ， ,m ，使 则向量是向量组A： , , ,    1 2 的一个线性组合， m 或称向量 可由向量组 A 线性表示． 课前复习

小结 a与ac1,a2,anm的关系为以下三种情院一： 1、a可由a1,a2,·,am线性表示，且表达式唯一， 2a可由a1,a2,am线性表示， 但不唯一， 如0,0)=（山，-1）+(1,1)=0(1，-1)+0(-1,1) 3不能由a1,2,anm线性表示元 区回

小结: , , , : 与1  2   m 的关系为以下三种情形之 一 1、 可 由1 , 2 ,  , m 线性表示， 且表达式唯一； 2、 可 由1 , 2 ,  , m 线性表示， 但不唯一， 如(0, 0) = (1, −1)+ (−1,1) = 0(1, −1)+ 0(−1,1) 3、 不能由1 ,2 ,  , m 线性表示

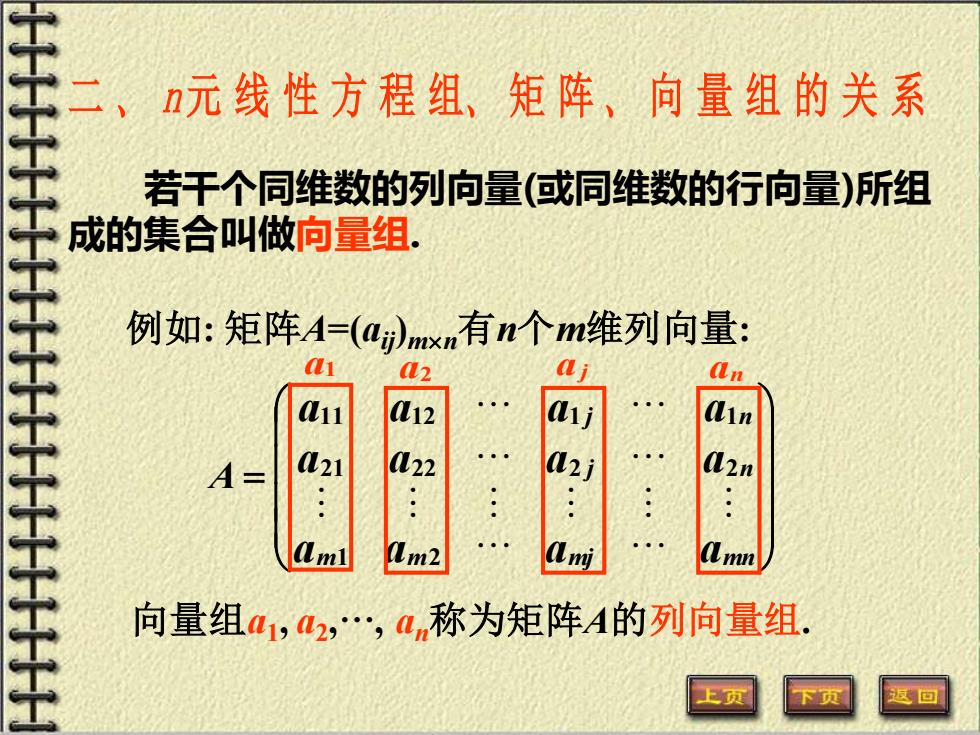
二、n元线性方程组、矩阵、向量组的关系 若干个同维数的列向量（或同维数的行向量）所组 成的集合叫做向量组. 例如：矩阵A-(amxw有n个m维列向量： 2 11 L12 A- 22 21 m2 mn 向量组m1,42,am称为矩阵A的列向量组

若干个同维数的列向量(或同维数的行向量)所组 成的集合叫做向量组. 例如: 矩阵A=(aij)mn有n个m维列向量:             = a a a a a a a a a a a a m m mj mn j n j n A             1 2 21 22 2 2 11 12 1 1 a1 a2 a j an 向量组a1 , a2 ,···, an称为矩阵A的列向量组. 二 、 n元线性方程组、 矩 阵 、 向量组的关系

类似地，矩阵A=(amxm有个n维行向量： 421422 a2n a A= a402 a aml am2 amn 向量组a,a必，am称为矩阵A的行向量组， 回

                = a a a a a a a a a a a a m m mn i i in n n A             1 2 1 2 21 22 2 11 12 1 1  向量组1 ’ , 2 ’ ,···, m ’称为矩阵A的行向量组. 类似地, 矩阵A=(aij)mn有m个n 维行向量:  2   i   m 