《线性代数》课程教学资源（PPT课件）第二章 矩阵及其运算 2.2 矩阵的运算

2、数乘矩阵的运算规律 (设A、B为mxn矩阵，2，u为数) ()()A=2(4 (2)(2+4)A=2A+4; (3)2(A+B)=2A+2B. 矩阵相加与数乘矩阵合起来，统称为矩阵的线 性运算

(1)()A = (A); (2)( + )A = A+ A; (3) (A+ B) = A+ B. 2、数乘矩阵的运算规律 矩阵相加与数乘矩阵合起来,统称为矩阵的线 性运算. （设 A、B 为 mn 矩阵，  , 为数）

三、矩阵与矩阵相乘 实例：某两种合金均含有某三种金属，其成分如下表： X Y Z 甲 0.8 0.1 0.1 0.4 0.3 0.3 现有甲种合金30吨，乙种合金20吨，求三种金属的数量 回

三、矩阵与矩阵相乘 实例：某两种合金均含有某三种金属，其成分如下表： 金 属 含 量 比 合 金 乙 0.4 0.3 0.3 甲 0.8 0.1 0.1 X Y Z 现有甲种合金30吨，乙种合金20吨，求三种金属的数量

分析：两种合金的成分构成矩阵记为： B-(888983 甲乙两种合金的重量构成的矩阵记为： A=(3020) 则三种金属的数量为： (3299)=AB 上页

分析：两种合金的成分构成矩阵记为:       = 0.4 0.3 0.3 0.8 0.1 0.1 B 甲乙两种合金的重量构成的矩阵记为: A= (30 20) 则三种金属的数量为: (32 9 9) = AB

1、定义 设A=(a,)是一个m×s矩阵，B=(b)是一个 S×n矩阵，那么规定矩阵A与矩阵B的乘积 是一个m×n矩阵C=(c,),其中 Cy=anby +ab++axby=Eanby (i=1,2,.m;j=1,2,n) 并把此乘积记作C=AB. 这回

１、定义 = + + + =  = s k ij ai b j ai b j ai sbsj ai k bkj c 1 1 1 2 2  (i = 1,2, m; j = 1,2,  ,n), 并把此乘积记作 C = AB. 设 是一个 矩阵， 是一个 矩阵，那么规定矩阵 与矩阵 的乘积 是一个 矩阵 ，其中 ( ) A = aij m s ( ) B = bij sn mn ( )ij C = c A B

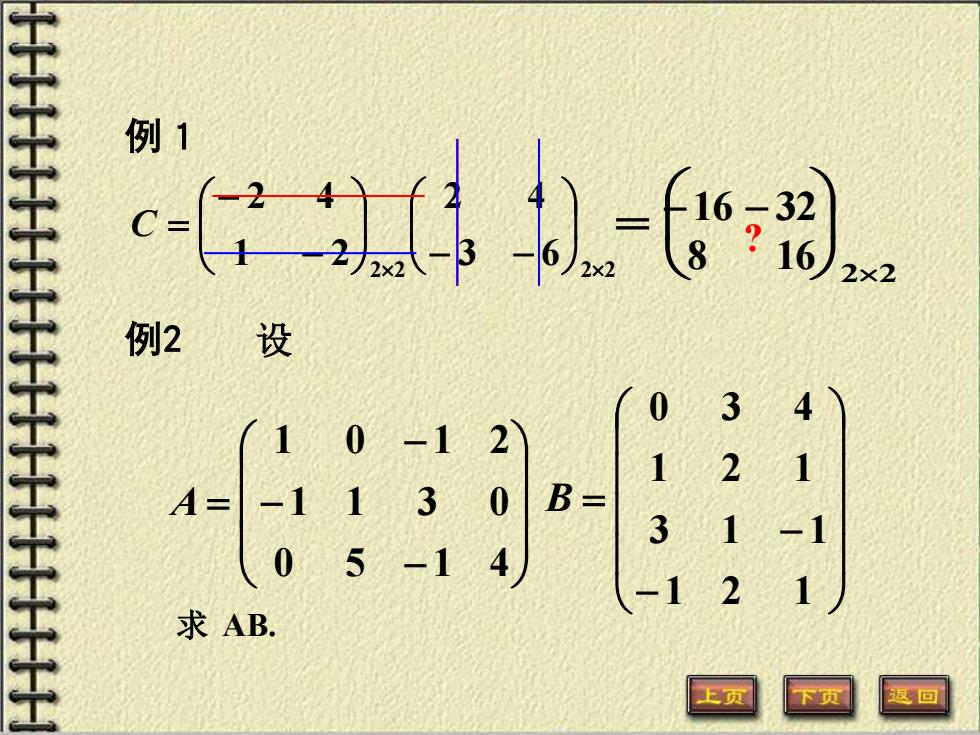
主王二二二二二干十二二二二 例1 一-周 例2 设 10 -1 2 2 A= -1 1 3 04 B= 013 1 5-1 41- 0 -1 2 求AB. 上页

例１ 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = −16 − 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ? 求 AB