
第一节向量组及其线性相关性 一、向量概念及表示方法 二、向量空间 三、向量、向量组与矩阵
第一节 向量组及其线性相关性 一、向量概念及表示方法 二、向量空间 三、向量、向量组与矩阵

n维向量的概念及表示方法 定义n个有次序的数a,a2,an所组成的数 组称为n维向量,这n个数称为该向量的n个分量, 第i个数a称为第个分量」 实向量:分量全为实数的向量。 复向量:分量为复数的向量
一、 n维向量的概念及表示方法 实向量:分量全为实数的向量。 复向量:分量为复数的向量。 1 2 , , , . n i n a a a n n n i a i 个有次序的数 所组成的数 组称为 维向量,这 个数称为该向量的 个分量, 第 个数 称为第 个分量 定义
例如 (1,2,3,.,m) n维实向量 1±2i2+3i,.,n+(n+1)i)→ n维复向量 第2个分量 第n个分量 第1个分量
例如 (1,2,3, ,n) (1 + 2i,2 + 3i, ,n + (n + 1)i) n维实向量 n维复向量 第1个分量 第n个分量 第2个分量
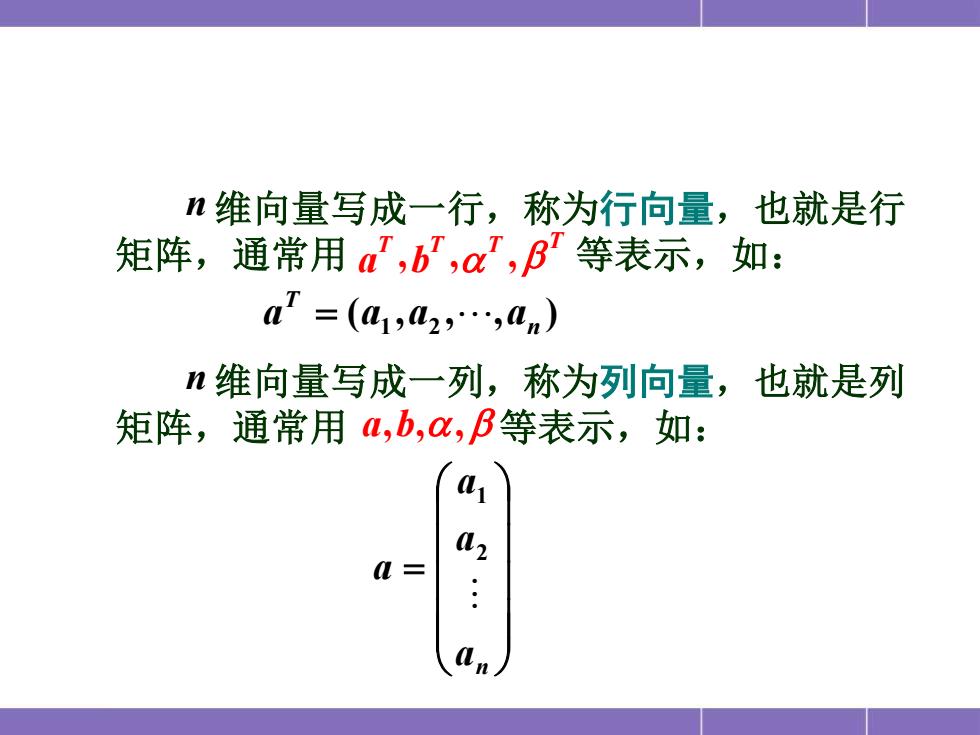
n维向量写成一行,称为行向量,也就是行 矩阵,通常用,b,a,β等表示,如: =(a1,02,.,0n) n维向量写成一列,称为列向量,也就是列 矩阵,通常用,b,u,B等表示,如: 01 02 a=
( , , , ) 1 2 n T a = a a a = an a a a 2 1 维向量写成一行,称为行向量,也就是行 矩阵,通常用 等表示,如: T T T T a ,b , , n 维向量写成一列,称为列向量,也就是列 矩阵,通常用 a,b,, 等表示,如: n

注意 1.行向量和列向量总被看作是两个不同的 向量 2.行向量和列向量都按照矩阵的运算法则 进行运算; 3.当没有明确说明是行向量还是列向量时, 都当作列向量:
注意 1.行向量和列向量总被看作是两个不同的 向量; 2.行向量和列向量都按照矩阵的运算法则 进行运算; 3.当没有明确说明是行向量还是列向量时, 都当作列向量