《线性代数》课程教学资源（PPT课件）第三章 矩阵的初等变换及线性方程组 3.1 矩阵的初等变换

第一节矩阵的初等变换 一消元法解线性方程组 二矩阵的初等变换 三初等矩阵 四初等矩阵的应用 五小结

第一节 矩阵的初等变换 五 小结 一 消元法解线性方程组 二 矩阵的初等变换 三 初等矩阵 四 初等矩阵的应用

一、消元法解线性方程组 分析：用消元法解下列方程组的过程. 求解线性方程组 2x1-X2-X3+x4=2, 七1+2-2x3+x4=4, o!a 4x1-6x2+2x3-2x4=4,③÷2 (1) 3x1+6x2-9x3+7x4=9,④

引例 (1) 一、消元法解线性方程组 求解线性方程组        + − + = − + − = + − + = − − + = 3 6 9 7 9, 4 6 2 2 4, 2 4, 2 2, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 分析：用消元法解下列方程组的过程．  2

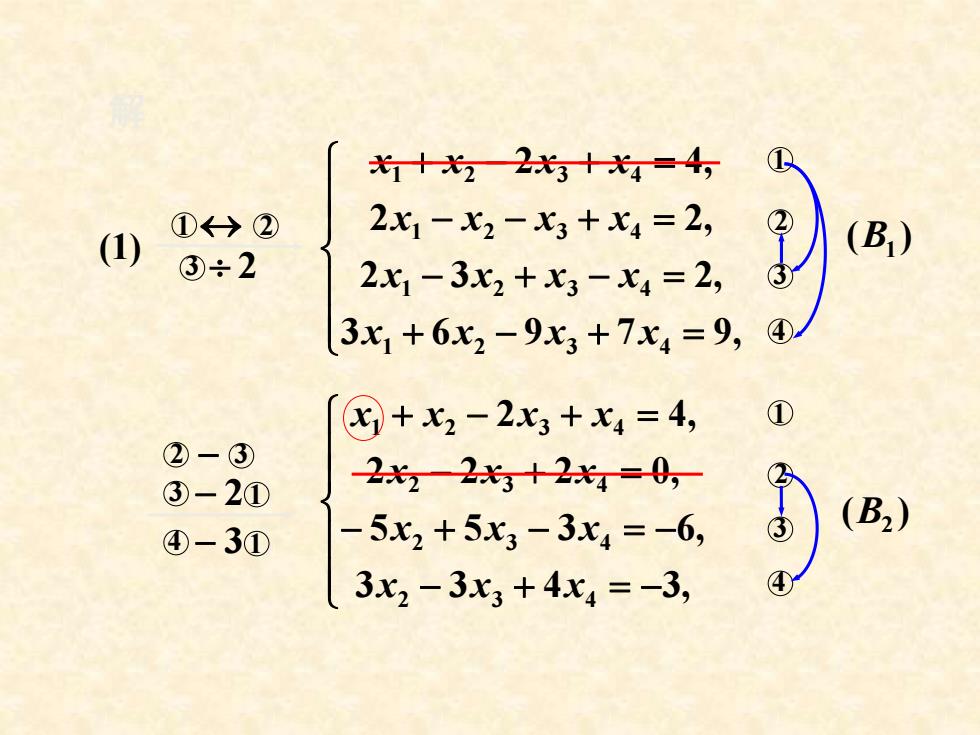
T+22x3十4=4， ① ①→② (1) 2x1-x2-53+x4=2, (B) ③÷2 2x1-3x2+X3-x4=2, 3x1+6x2-9x3+7x4=9, ④ 8+x2-2X+x4=4, ① ②-③ ③-2① 2x2—23+2xx=0, ④-3① 5x2+5x3-3x4=-6, (B2) 3x2-3x3+4x4=-3, ④

解 ( ) (1) B1 ( ) B2   2 1 3 2        + − + = − + − = − − + = + − + = 3 6 9 7 9, 2 3 2, 2 2, 2 4, 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x x x x x 1 3 4 2 − 2 1 2 − 3 3 4 − 3 1        − + = − − + − = − − + = + − + = 3 3 4 3, 5 5 3 6, 2 2 2 0, 2 4, 2 3 4 2 3 4 2 3 4 1 2 3 4 x x x x x x x x x x x x x 1 3 4 2

1 X1+x2-2x3+x4=4,① ②× 2 83-七3+X4=0, ③+5② (B3) 2X4=-6, ④-3② x4=-3, X1+X2-2x3+X4=4, ① ③←→④ x2-x3+x4=0, ② (B4) ④-2③ 0=-3. ③ 0=0, ④ 用“回代”的方法求出解：

( ) B3 ( ) B4        = − = − − + = + − + = 3, 2 6, 0, 2 4, 4 4 2 3 4 1 2 3 4 x x x x x x x x x 1 3 4 2 + 5 2 2 1  3 4 − 3 2 2        = = − − + = + − + = 0 0, 3, 0, 2 4, 4 2 3 4 1 2 3 4 x x x x x x x x 1 3 4 3  2 4 − 2 4 3 用“回代”的方法求出解：

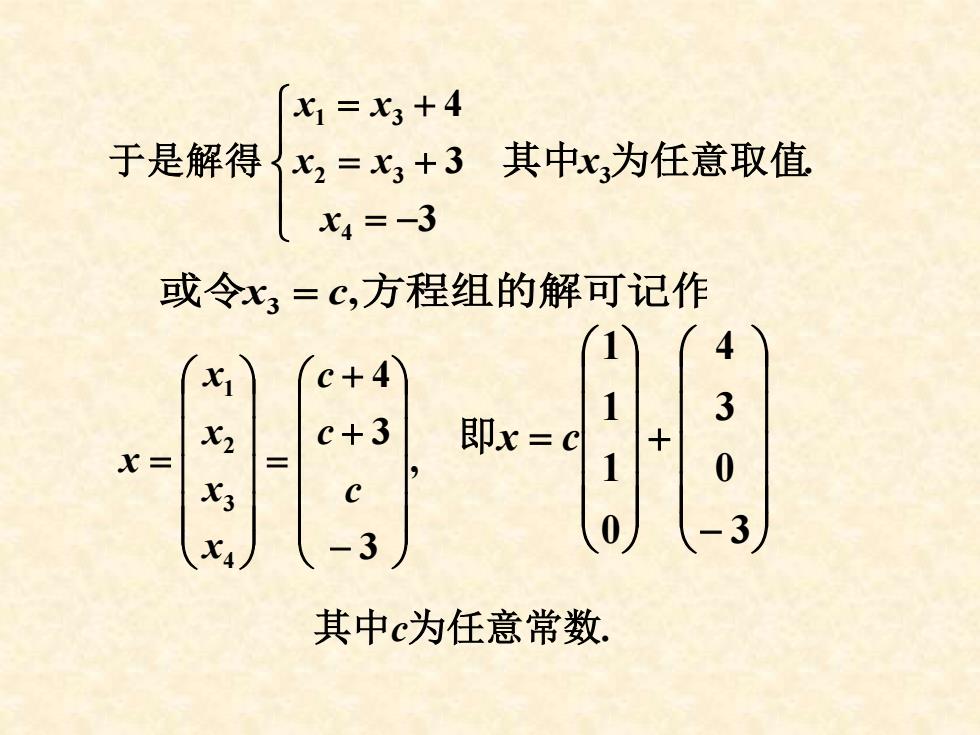
1=X3+4 于是解得x2=x,+3其中x为任意取值 X4=-3 或令x3=c,方程组的解可记作 c+4 1 X2 c+3 即x=c x= X3 -3 其中c为任意常数

于是解得      = − = + = + 3 3 4 4 2 3 1 3 x x x x x . 其中x3为任意取值 或令x3 = c,方程组的解可记作 , 3 3 4 4 3 2 1               − + + =               = c c c x x x x x 其中c为任意常数.               − +               = 3 0 3 4 0 1 1 1 即x c