
练习:P23题8用向量证明直径所对圆周角是直角 练习:P23题2 机动目录上页下页返回结抹
机动 目录 上页 下页 返回 结束 练习:P23 题 8 用向量证明直径所对圆周角是直角. 练习:P23题2

4.数量积的坐标表示 设a=ai+a,j+a.k,b=b,i+b,j+bk,则 a.B=(axi+ay j+az k)-(bxi+by J+b-K) ii=jj=k=1,7=了k=k7=0 a.b=axbx ayby +a-b= 两向量的夹角公式 当a,b为非零向量时,由于a.b=acos0,得 a.b axbx ayby a-b- c0S0= b+ b2+ 8
4. 数量积的坐标表示 设 则 = 0 x x y y z z = a b + a b + a b 当 为非零向量时, cos = = x x y y z z a b + a b + a b 2 2 2 x y z a + a + a 2 2 2 x y z b + b + b 由于 a b cos a a i a j a k , = x + y + z b b i b j b k , = x + y + z ( a i + a j + a k ) x y z (b i b j b k ) x + y + z i j = j k = k i a b a b 两向量的夹角公式 , 得 机动 目录 上页 下页 返回 结束

aLb→ab+ab,+ab=0 例3 已知a=(1,1,-4),b=(1,-2,2),求(1) a.B: (2)a与b的夹角;(3)在b上的投 影. 解 (①)a.b=11+1.(-2)+(-4)2=-9. axbs +a,bya,b. 2)c0s0= a2+a,2+a:Vb2+b,2+b1 2 ③4-5-51@x@- a.b =-3 目录上页下页返回结辣
例 3 已知a = (1,1,−4) ,b = (1,−2,2) ,求(1) a b ;(2)a 与 b 的夹角;(3) a 在 b 上的投 影. 解 a b (1) = 11 + 1(−2) + (−4) 2 = −9. 2 2 2 2 2 2 (2) cos x y z x y z x x y y z z a a a b b b a b a b a b + + + + + + = , 2 1 = − b a b b a (3) =| | ( ) 3. | | ( ) = − = b a b a b 机动 目录 上页 下页 返回 结束 a ⊥ b ax bx + ay by + az bz = 0
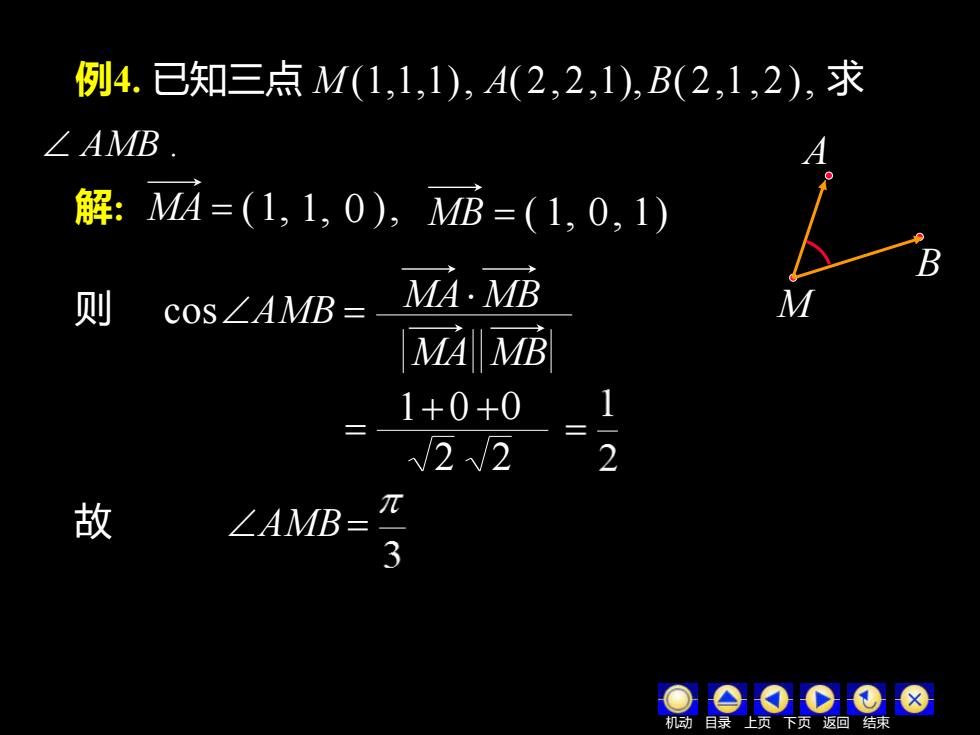
例4.已知三点M(1,1,1),A(2,2,1),B(2,1,2),求 ∠AMB. 解:MA=(1,1,0),MB=(1,0,1) 则 CoS∠AMB= MA·MB MAMB 1+0+0 22 故 ∠AMB= 8 结
MA = ( ), MB = ( ) = B M 例4. 已知三点 M (1,1,1), A( 2, 2,1), B( 2,1 , 2), AMB . A 解: 1, 1, 0 1, 0, 1 则 cosAMB = 1+ 0 +0 2 2 AMB= 求 MA MB MA MB 故 机动 目录 上页 下页 返回 结束

那,已知向a,5的夹角9-且@迈,11=3 求a-b. 解:a-b2=(a-b)(a-b) =a-a-2a-b+b.b =la2-2aBc050+B2 3π =v22-223cos年+3 =17 .a-b=17 上页下页返回结束
2 2 3 4 3 = ( 2) − 2 2 3 cos + =17 例5. 已知向量 的夹角 且 解: , 4 3 a , b = | a | = 2, | b | = 3, ( a − b )( a − b ) = a a + b b 2 2 = a − 2 a b cos + b a − b = 17 机动 目录 上页 下页 返回 结束