
上讲提要 1.导数的概念、几何意义、物理 意义; 2.可导与连续的关系; 3.导数的四则运算 。 3
3 上讲提要 1.导数的概念、几何意义、物理 意义; 2.可导与连续的关系; 3.导数的四则运算

第二节 初等函数的导数 三、反函数的求导法则 定理2-1若函数x=p(y)在y点的某邻域内单调,可导, 且p'(y)≠0,则它的反函数y=f(x)在x点(x=p(y)处可 导,且 f(x)=1 p'(y) 简单地说,反函数的导数等于直接函数的导数的倒数。 例1已知y=aresin(-1<x<L-子<y<7求. 解 少=cmx是x=smy的反两数:=smy布(受受 单调、可导,且siny)'=cosy>0,故在(-1,1)内有
4 第二节 初等函数的导数 定理2-1 若函数 x y = ( )在 y 点的某邻域内单调,可导, 且 ( ) 0 y ,则它的反函数 y f x = ( )在x点( x y = ( ))处 可 导,且 1 ( ) ( ) f x y = 简单地说,反函数的导数等于直接函数的导数的倒数。 三、反函数的求导法则 例1 已知 y x = arcsin ( 1 1, ) 2 2 x y − − ,求 y 。 解 y x = arcsin 是x y = sin 的反函数。x y = sin 在( , ) 2 2 − 单调、可导,且(sin ) cos 0 y y = ,故在( 1,1) − 内有
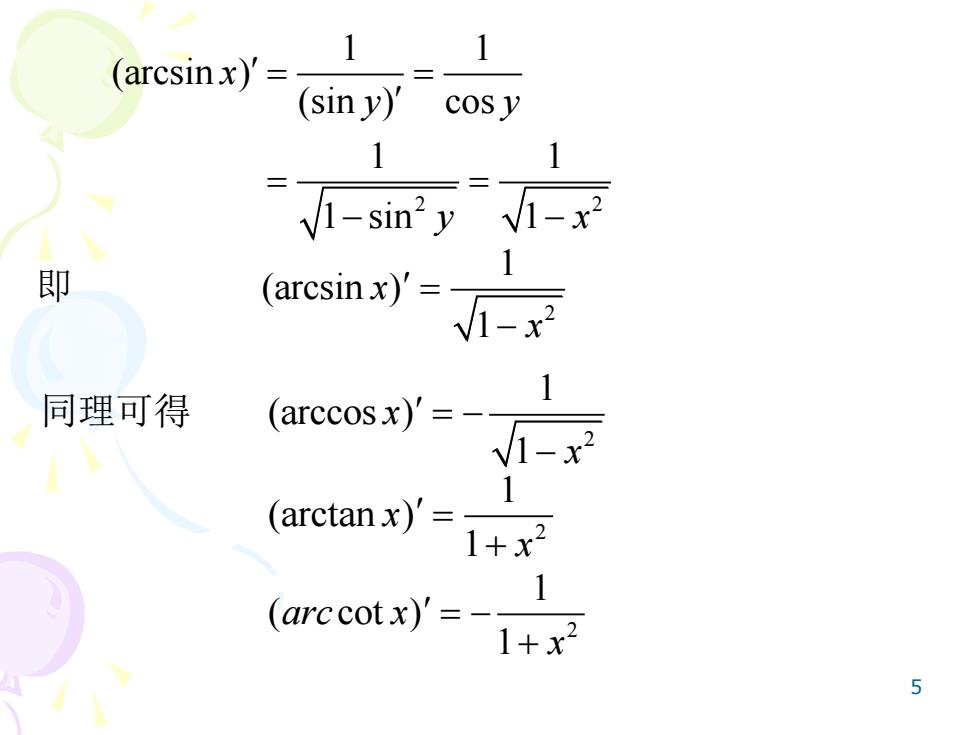
1 (arcsinx)'= (siny)' cos v 1 1-sin2y v1-x2 即 (arcsinx) 1-x 同理可得 (arccosx)'=-- 1 1-x2 (arctanx)= (arccotx)'=- 1 +x2 5
5 2 2 1 1 (arcsin ) (sin ) cos 1 1 1 sin 1 x y y y x = = = = − − 即 2 1 (arcsin ) 1 x x = − 同理可得 2 1 (arccos ) 1 x x = − − 2 1 (arctan ) 1 x x = + 2 1 ( cot ) 1 arc x x = − +

例2已知y=a(a>0且a≠1),求y'。 解已知y=a是x=loga y的反函数, 而x=log。y在(0,+o)上单调可导,且 (log。yy= ≠0 ylna 故在相应的区间(-0,+0)内,有 (a)y= ylna=a*Ina (log,y)' 即 (a")'=a"Ina 特别,a=e时,有 (e)'=e。 四、复合函数的求导法则 定理2-2(锁链法则)设函数u=0(x)在x点处可导,而函数
6 例2 已知 x y a = ( a 0且a 1 ),求 y 。 解 已知 x y a = 是 loga x y = 的反函数, 而 loga x y = 在(0, ) + 上单调可导,且 1 (log ) 0 ln a y y a = 故在相应的区间( , ) − + 内,有 1 ( ) ln ln (log ) x x a a y a a a y = = = 即 ( ) ln x x a a a = 特别,a e = 时,有 ( ) x x e e = 。 四、复合函数的求导法则 定理 2-2 (锁链法则)设函数u x = ( )在x点处可导,而函数

y=f(u)在x点对应的u(u=p(x)点处可导,则复合函数 y=f(p(x)在x点处可导,且其导数为 [f(p(x)]'=f'(wW)p'(x) 或 dydy du dx du dx 证明给x一增量△x,则相应地有函数u=p(x)的增量 △u,函数y的增量△y。己知函数y=f()在u点可导,则有 lim Ay=f'(u)(Au≠0) Au-→0△W 故 y =f'(w0+a △u 其中lim a=0, △1M->0 7
7 y f u = ( )在 x 点对应的 u u x ( ( )) = 点处可导,则复合函数 y f x = ( ( )) 在x点处可导,且其导数为 [ ( ( ))] ( ) ( ) f x f u x = 或 dy dy du dx du dx = 证 明 给 x 一增量x ,则相应地有函数 u x = ( )的增量 u,函数y的增量y 。已知函数y f u = ( )在u点可导,则有 0 lim ( ) u y f u → u = ( u 0) 故 ( ) y f u u = + 其中 0 lim 0 u → =