
主讲摘要 1.复合函数求导法则; 2.隐函数求导法则,对数求导法。 3
3 主讲摘要 1.复合函数求导法则; 2.隐函数求导法则,对数求导法

第二节初等函数的导数 八、高阶导数 函数y=f(x)的导数y'=f'(x)仍然是x的函数。将 得 y'='(x)的导数,称为函数y=f(x)的二阶导数,记为 y,f"(x),9 dx2 类似,如果y”=f"(x)可导,则它的导数称为y=f(x) 的三阶数严或 dx3 若函数y=f(x)的n-1阶导数仍然可导,则它的导
4 第二节 初等函数的导数 八、高阶导数 函 数 y f x = ( )的导数 y f x = ( ) 仍然是 x 的函数。将 y f x = ( )的导数,称为函数y f x = ( )的二阶导数,记为 y , f x ( ), 2 2 d y dx 或 2 2 d f x( ) dx 类似,如果 y f x = ( )可导,则它的导数称为y f x = ( ) 的三阶导数,记为y , f x ( ), 3 3 d y dx 或 3 3 d f x( ) dx 。 若函数y f x = ( )的n −1阶导数仍然可导,则它的导

数,称为y=f(x)的n阶导数,记为 mf(x.42或f dx” x" 二阶及二阶以上的导数,统称为高阶导数。 二阶导数的物理意义 变速直线运动路程函数为S=s(t),v=s'(t)为瞬时 速度,a=v'(t)=s"(t)为加速度。 例1已知n次多项式D(x)=ax”+ax+…+an-2x2+an1x+an, 求Pn(x)的各阶导数。 解P(x)=nax+(n-1)a,x-2+…++2an-2x+a- P(x)=nn-1)a"-2+(n-10(n-2)a,x"-3+…+2an-2
5 数,称为y f x = ( )的n阶导数,记为 ( ) n y , ( ) ( ) n f x , n n d y dx 或 ( ) n n d f x dx 二阶及二阶以上的导数,统称为高阶导数。 二阶导数的物理意义 变速直线运动路程函数为s s t = ( ),v s t = ( )为瞬 时 速度,a v t s t = = ( ) ( )为加速度。 例1 已知n次多项式 1 2 0 1 2 1 ( ) n n P x a x a x a x a x a n n n n − = + + + + + − − , 求 ( ) P x n 的各阶导数。 解 1 2 0 1 2 1 ( ) ( 1) 2 n n P x na x n a x a x a n n n − − − − = + − + + + + 2 3 0 1 2 ( ) ( 1) ( 1)( 2) 2 n n P x n n a x n n a x a n n − − − = − + − − + +
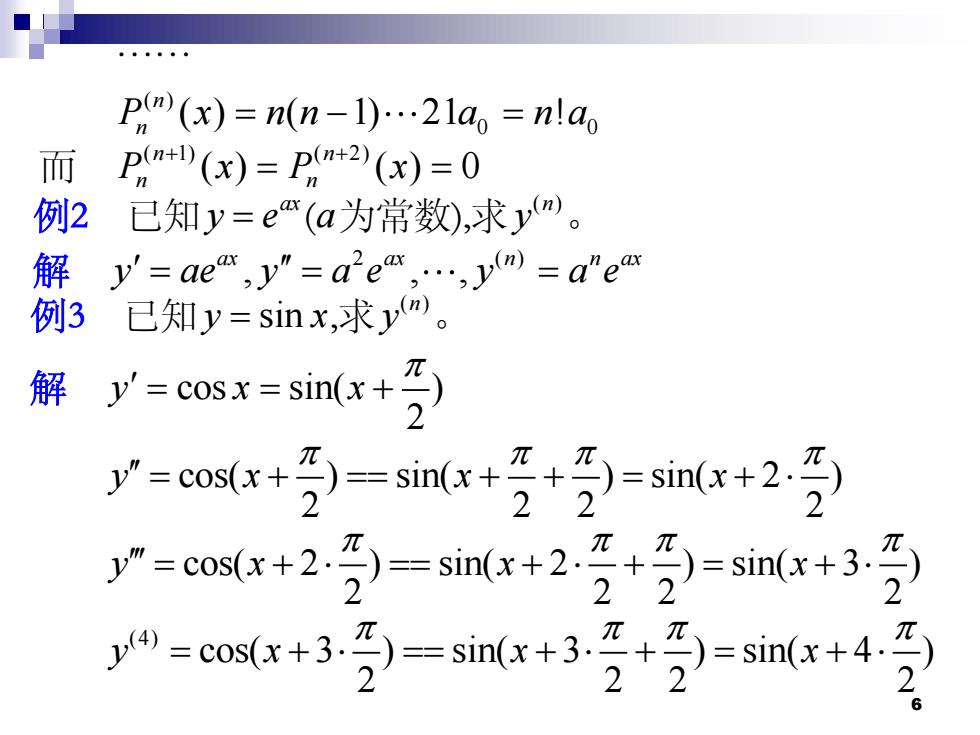
p((x)=n(n-1)...21ao=nlao 而pm+(x)=Pm2》(x)=0 例2已知y=e(a为常数),求ym。 解y'=aem,y"=ae“,…,ym=ae 例3已知y=sinx,求ym。 y=cosx=sin(x+) 解 =x+7=sm+经+=snx+2 y"=cos(x+2.7)=sin(x+2.7+7)=sin(x+3.7) π 2· =n+4 =cax+33=sn+3号+ 1
6 ……( ) 0 0 ( ) ( 1) 21 ! n P x n n a n a n = − = 而 ( 1) ( 2) ( ) ( ) 0 n n P x P x n n + + = = 例2 已知 ax y e = (a为常数),求 ( ) n y 。 解 2 ( ) , , , ax ax n n ax y ae y a e y a e = = = 例3 已知 y x = sin ,求 ( ) n y 。 解 cos sin( ) 2 y x x = = + cos( ) sin( ) sin( 2 ) 2 2 2 2 y x x x = + == + + = + cos( 2 ) sin( 2 ) sin( 3 ) 2 2 2 2 y x x x = + == + + = + (4) cos( 3 ) sin( 3 ) sin( 4 ) 2 2 2 2 y x x x = + == + + = +

y)=sin(x+n. 即nm=snx+n 同理可得(eosx=co(+n受 例4.y=ln(1+x),求y。 解 1+x (1+x)2 1.2 y"= 123 31 (1+x)3 (1+x)4 =(103 (1+x)4 7
7 …… ( ) sin( ) 2 n y x n = + 即 ( ) (sin ) sin( ) 2 n x x n = + 同理可得 ( ) (cos ) cos( ) 2 n x x n = + 例4.y x = + ln(1 ),求 ( ) n y 。 解 1 1 y x = + 2 1 (1 ) y x = − + 3 1 2 (1 ) y x = + (4) 3 4 4 1 2 3 3! ( 1) (1 ) (1 ) y x x = − = − + +