吉林大学：《医用高等数学》课程电子教案（PPT课件）第四章 多元函数微积分学（6/6）

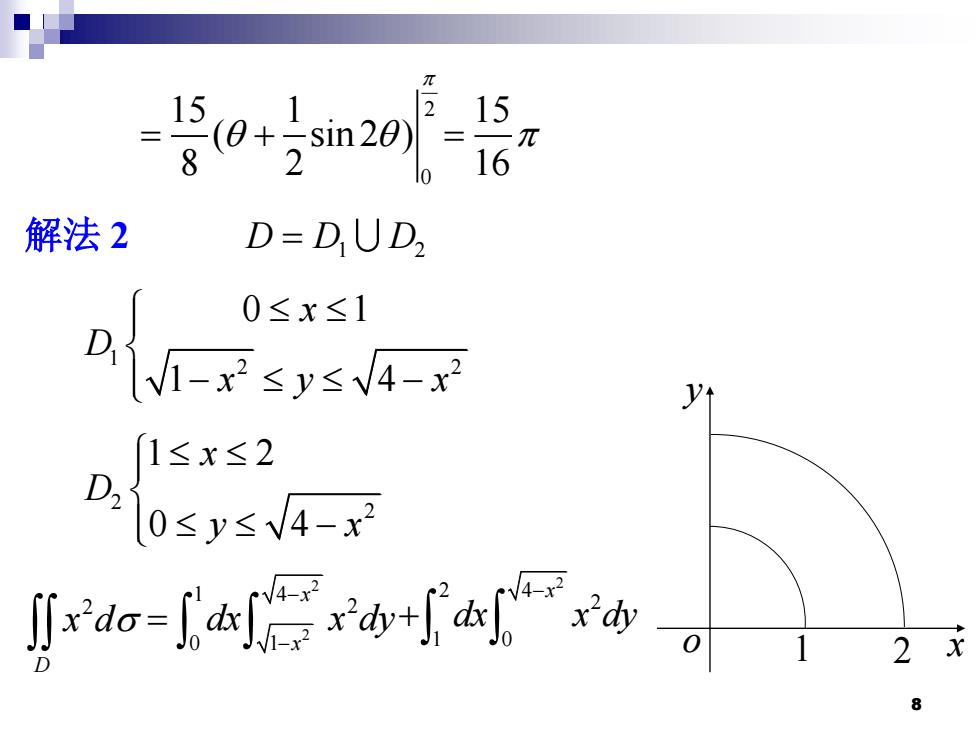
-15(+sim2 215 i16 元 8 2 解法2 D=DUD, Dve 0≤x≤1 1≤x≤2 D0≤y≤N4-r xdo-xay-f db 3-0 2尤 8

8 2 0 15 1 ( sin 2 ) 8 2  = +   15 16 =  解法 2 D D D = 1 2 1 2 2 0 1 1 4 x D x y x       −   − 2 2 1 2 0 4 x D y x         − 2 D x d  2 2 1 4 2 0 1 x x dx x dy − − =   2 2 4 2 1 0 x dx x dy − +  o y 1 2 x

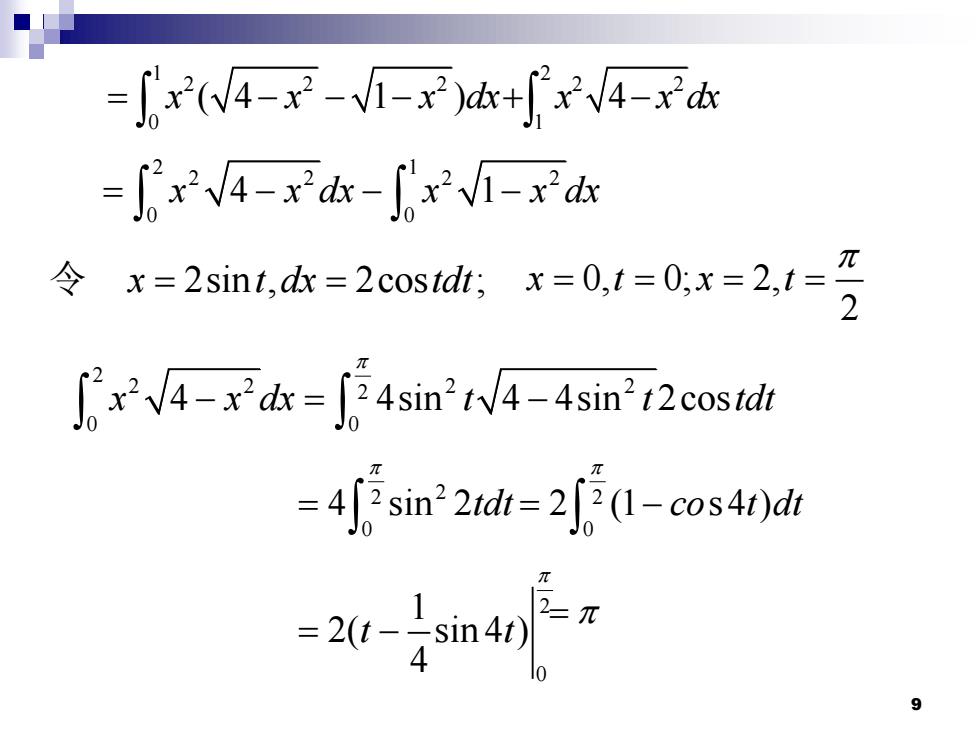
=∫(4-2-V-)d+2xV4-d -fx14-xdx-fxf-xdx x=2sint,dx =2costdt;x=0,t=0;x=2,t= π 4sin4-4sin12cosidt 4 sin?21dt-2(1-cos4r)dr = 9

9 1 2 2 2 0 = − − − x x x dx ( 4 1 )  2 2 2 1 + − x x dx 4  2 1 2 2 2 2 0 0 = − − − x x dx x x dx 4 1   令 x t dx tdt = = 2sin , 2cos ; 0, 0; 2, 2 x t x t  = = = = 2 2 2 2 2 2 0 0 4 4sin 4 4sin 2cos x x dx t t tdt  − = −   2 2 0 4 sin 2tdt  =  2 0 2 (1 s4 ) co t dt  = −  2 0 1 2( sin 4 ) 4 t t  = − = 

令 x=sint,dx costdt x=0,1=0x=l1=2 dx=sin-sin'i costdt -sm2h 0rdo=r4-k-小x-平dk π15π =π 1616 10

10 令 x t dx tdt = = sin , cos 0, 0; 1, 2 x t x t  = = = = 1 2 2 2 2 2 0 0 x x dx t t tdt 1 sin 1 sin cos  − = −   2 2 0 1 sin 2 4 tdt  =  2 0 1 (1 s4 ) 8 co t dt  = −  16  = 2 D x d  2 1 2 2 2 2 0 0 = − − − x x dx x x dx 4 1   15 16 16   = − = 

例2.求川e+do,区域D={(x,)川1≤x2+y2≤9且y≥x π 5π ≤0≤ 解 4 1≤p≤3 所t以eda-dof po X =7e-e 11

11 例 2．求 2 2 x y D e d +  ，区域 2 2 D x y x y y x =  +   {( , ) |1 9 } 且 解 5 4 4 1 3 D              所以 2 2 x y D e d +  2 5 3 4 1 4 d e d   =       2 3 1 5 1 4 4 2 e      = −     9 ( ) 2 e e  = − x y o

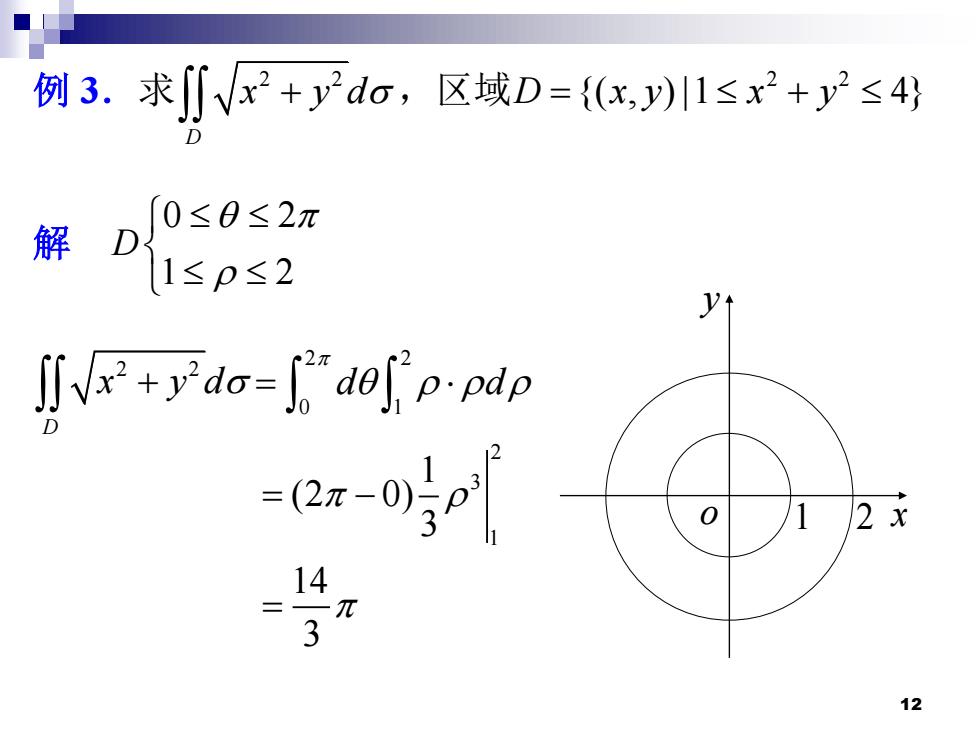
例3.求∬Vx2+ydo,区域D={(x,川1≤x2+y2≤4 解 ∫0≤8≤2π D51≤p2 d-["do"p.pdp =2x-n5 1 2 x 12

12 例 3．求 2 2 D x y d +   ，区域 2 2 D x y x y =  +  {( , ) |1 4} 解 0 2 1 2 D           2 2 D x y d +   2 2 0 1 d d  =        2 3 1 1 (2 0) 3 14 3    = − = x y o 1 2