
·30· 第1章n阶行列式 -1 0 .0 0 0 -1.0 0 (5) =x+a1x+.+ar1x十an 00.x -1 a2 x十a x31 x+2y-4 -2 5.已知y0-2 1,求 3 2 x2-1 1 1 6.在六阶行列式中,amananas6a14a6和as1aaga1asas 这两项应是什么 符号? 7.已知五阶行列式第一列元素分别为一1,1,3,x,4:第二列元素对应的代数 余子式依次为3,4,2,5,7,求x 8.已知 213-5 23 D 1 111 2 749 2 求A1+A2十Ag+A4 9.计算下列行列式的值 - 11 2-12 0 1 (1) 2 (2) 1 -2 0 53 ; -2 -4 1 6 3111 0b0 1311 (3) 1131 (4) 0 c o d 0 x o 1113 1 -1 1 x-1 1 1 (5) x+1 -1 1 -1 x+1
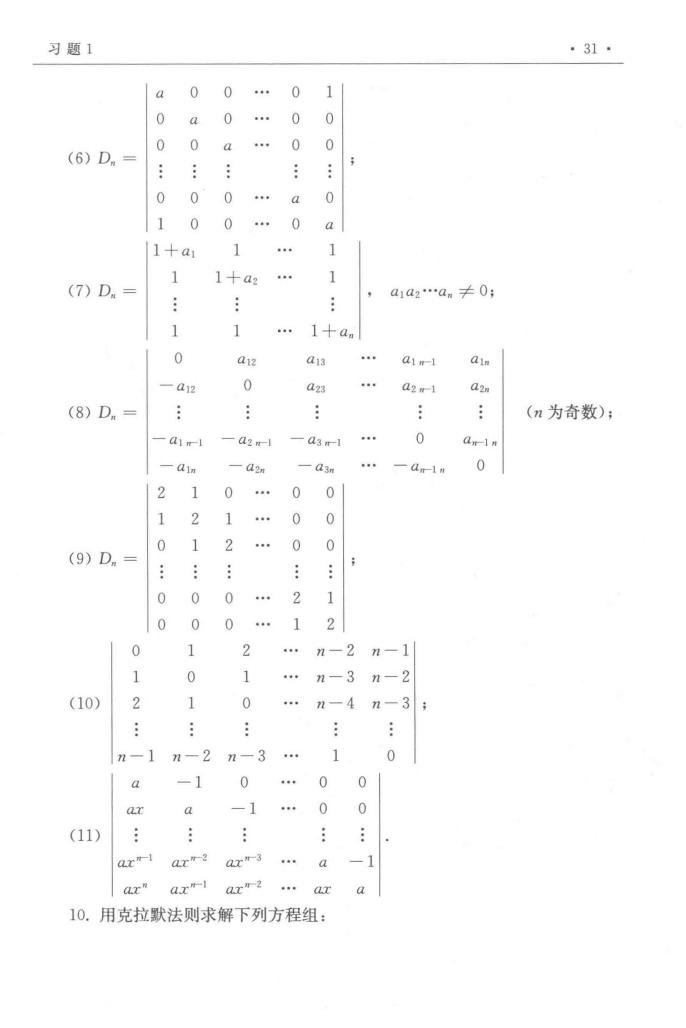
习题1 ·31 a00.01 0a0.00 (6)D.= 00a.00 000 a 0 100.0 a 1+a 1 . 1 1 (7)D.= 1+a a1a2.an≠0: 1 1 .1十am 0 a12 an . a1-1 din 0 an a2g-1 (8)D.= (n为奇数); A1m-1 一ag一agmr1. 0 d2m -a3n . 一a-1 0 1 0.00 1 2 1. 0 0 (9)D.= 0 1 2 . 0 0 0 0 0 2 0 0 0 1 2 0 2 n-2n-1 1 n -3 n-2 (10) 2 1 0 n-4 n-3 n-1n-2n-3. 0 a -1 0.0 0 a -1.0 (11): ar-laxr-2ax"-3.a arna.x-laxr2.ax a 10.用克拉默法则求解下列方程组:

·32· 第1章n阶行列式 x十y+x=0, (1){2x-5y-3z=10, 2x+4y+z=2: 2x1+2-5m+x4=8, (2) x1-3x2-6z4=9, 2x2-x3十2x4=-5, x1+4x2-7x3+6x4=0: 2x1-x2+3x+2=6, (3) 3x1-3x2+3x3+2x4=5, 3x1-2-+2x=3, 3x1-x2+3x-x4=4: x1+2x2-2x3+4x4-x5=-1, 2x1-x+3x3-4x4+2x=8, (4){3x1+x2-x4+2x4-x5=3, 4x1+3.x2+41+2x4+2x6=-2, x1-x2-x3+2x4-3x5=-3; x1十x2十.十xn=1, a1x1十a2x2十.十amx。=b, (5)aix1+aix2+.+ax。=b, 440444400000 alx1十ax十.十axm=l, 其中a,.,an互不相等. 11.若三次多项式f(x)=ax3十a2x2十a1x十a,当x=1,2,3,-1时,其 值分别为一3,5,35,5,试求f(x)在x=4时的值. 12.某工厂生产甲、乙、丙三种钢制品,已知甲、乙、丙三种产品的钢材利用率 分别为60%,70%,80%,年进钢材总吨位为100万吨,年产品总吨位为67万吨,此 外甲、乙两种产品必须配套生产,乙产品成品总重量是甲产品总重量的70%,此外 还已知生产甲、乙、丙三种产品每吨可获利分别为1万元,1.5万元、2万元,问该工 厂本年度可获利润多少元? 13.问入取何值时,齐次线性方程组 (0+3)+x+2x=0, 江1+(A-1)x2十x=0, 3(1+1)x1+x2+(+3).x3=0 有非零解?

习题1 .33· 14,证明无论a取何值,线性方程组 (a2-2)x1+x2-2x1=0, -5x1+(a3+3)x-3x4=0, x1+(a2-2)x3=0 只有零解

第2章矩阵与向量 向量空间和矩阵的理论组成了线性代数的基本内容.本章将重点介绍向量组 的线性相关性以及矩阵的秩的概念,并通过矩阵的初等变换对这两个基本问题进 行讨论. 2.1消元法与矩阵的初等变换 在中学代数里我们学过用加减消元法解二元及三元线性方程组.实际上,用消 元法比用行列式解线性方程组更具有普遍性,为了说明这一点,下面我们通过一个 例子来考察加减消元法解线性方程组的一般规律. 设有三元线性方程组 2x1-x2+2x3=4, x1+x2+2.x3=1, (2.1) 4x1+x2+4x=2. 先将方程组的第一,二两个方程的位置互换,得到 x1+x2十2x=1, 21-x2+2x=4 (2.2) 4x1+x+4x3=2. 将方程组(2.2)的第一个方程的一2倍加到第二个方程上,一4倍加到第三个方程 上,得到 x1+x2+2x1=1, -3x2-2x3=2, (2.3) -3x2-4x3=-2. 将方程组(2.3)的第二个方程的一1倍加到第三个方程上,得到 (x+x2+2x3=1, -3x2-2x=2, (2.4) -2x3=-4 再将方程组(2.4)的第三个方程的一1倍加到第二个方程上,十1倍加到第一个方 程上,得到