
复变函数定理二设 lim f(z) = A, lim g(z)= B,那末ZZOZ→Z0(1) lim[f(z)±g(z)) = A± B;Z→ZO(2)1lim[f(z)g(z)] = AB;Z-→ZoAf(z)lim(3)(B ± 0).Bg(z)z>Z0与实变函数的极限运算法则类似u
6 定理二 ( 0). ( ) ( ) (3) lim (2) lim[ ( ) ( )] ; (1) lim[ ( ) ( )] ; lim ( ) , lim ( ) , 0 0 0 0 0 = = = = = → → → → → B B A g z f z f z g z AB f z g z A B f z A g z B z z z z z z z z z z 设 那 末 与实变函数的极限运算法则类似
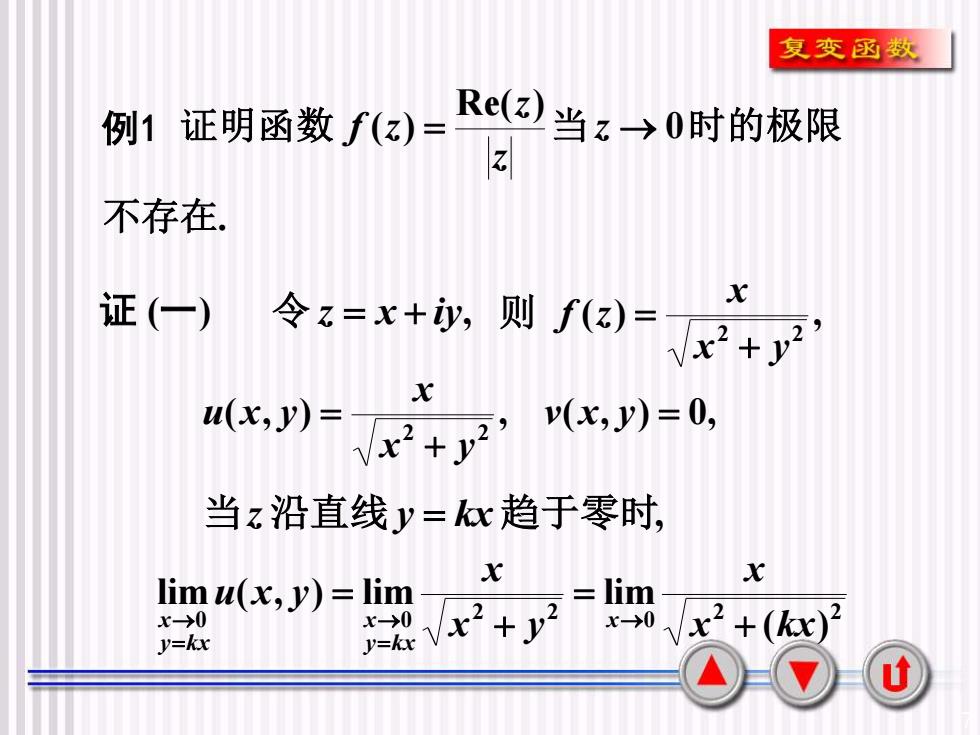
复变函数Re(z)当→0时的极限例1 证明函数 f(z)=N不存在。x证(一)令z=x+iy,则 f(z)=2Vx? + yxu(x,y) =v(x,y) = 0,x?+ y?当z沿直线y=kx趋于零时,xxlim u(x, y) = limlim222x-→0x-0x-0+(kx)Vx+yXy=kry=kxU
7 例 1 证 ( 一 ) . 0 Re( ) ( ) 不存在 证明函数 = 当z → 时的极限 z z f z 令 z = x + iy, ( ) , 2 2 x y x f z + 则 = ( , ) , ( , ) 0, 2 2 = + = v x y x y x u x y 当z 沿直线 y = kx 趋于零时, 2 2 0 0 lim ( , ) lim x y x u x y y k x x y k x x + = =→ =→ 2 2 0 ( ) lim x kx x x + = →