
例2.已知方程siny+e-xy-1=0在点(0,0)某邻域 确定一个单值可导隐函数y=∫(x),求 dy d2y dxx=0 dx2x=0 解:令F(x,y)=siny+e'-xy-l,则 F=ex-y,Fy=cosy-x ex-y dx F cOS y-x dy x=0= ex-y =-1 cOSy-xx=0,y=0
山东农业大学 高等数学 主讲人:苏本堂 例2. 已知方程 在点(0,0)某邻域 确定一个单值可导隐函数 d 0 d , d 0 d 2 2 = x x = y x x y 解: 令 F(x, y) = sin y + e − xy −1, x F e y, x x = − 则 F y x y = cos − 求 x y d d y x F F = − = − cos y − x e y x − d 0 d x x = y = − cos y − x e y x − x = 0, y = 0
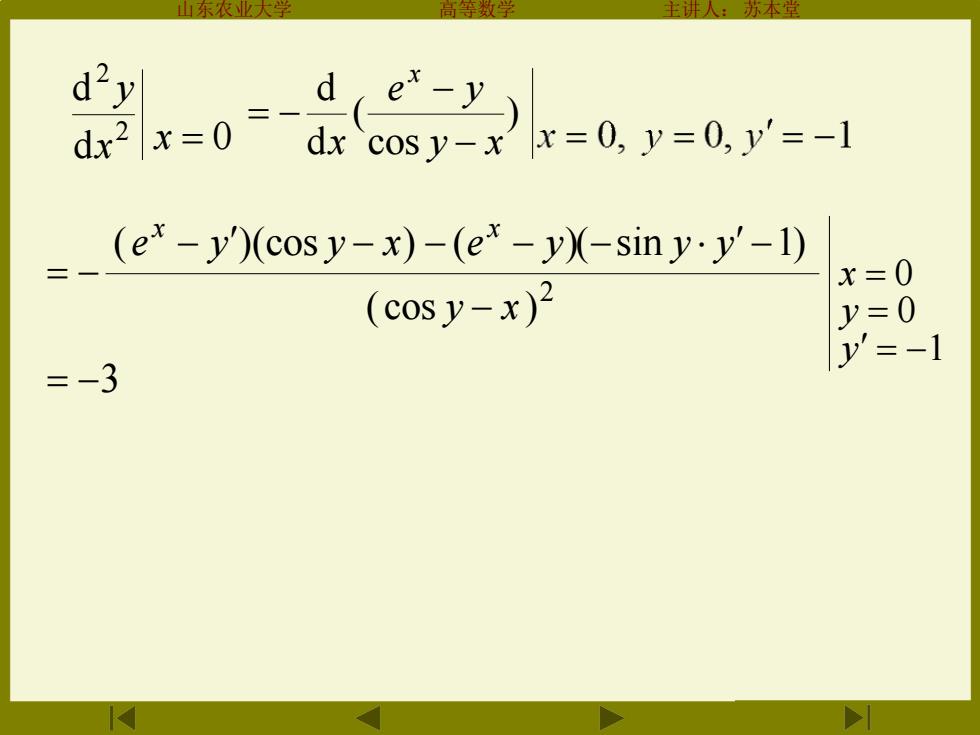
主计 本 d2y d e-y) x=0=dxcosy-x=0,y=0,y'=-1 (e*-y)(cosy-x)-(e*-y)-siny.y'-1) x=0 (cosy-x)2 y=0 y'=-1 =-3
山东农业大学 高等数学 主讲人:苏本堂 d 0 d 2 2 x x = y ) cos ( d d y x e y x x − − = − 2 ( cos ) y − x = − = −3 1 0 0 = − = = y y x (e y ) x − (cos y − x) (e y) x − − (−sin y y −1)