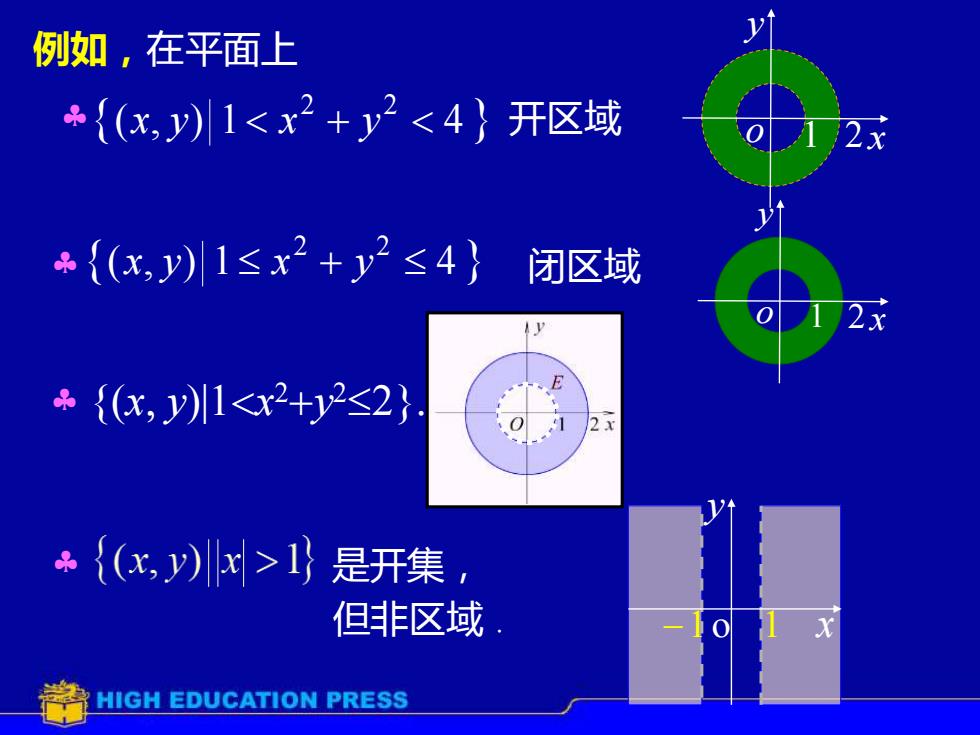
例如,在平面上 {(x,y)1<x2+y2<4}开区域 {(x,y)1≤x2+y2≤4}闭区域 {(,y1<x2+2≤2} 2 ÷{(x,y)x>1是开集 但非区域 HIGH EDUCATION PRESS
例如,在平面上 ( , ) 1 4 2 2 x y x + y ( , ) 1 4 2 2 x y x + y 开区域 闭区域 x y o 1 2 x y o 1 2 {(x y)|1x 2+y 2 2} 是开集, 但非区域 . −1 o 1 x y

(4)有界集无界集 ·有界集对于平面点集E,如果存在某一正数r,使得 ECU(O,r), 其中O是坐标原点,则称E为有界点集 无界集一个集合如果不是有界集,就称这集合为无界集 举例 点集{x,y1≤x2+2≤4}是有界闭区域, 点集{x,y)x+>1}是无界开区域; 点集{(x,y)川x+21}是无界闭区域 HIGH EDUCATION PRESS
◆有界集 对于平面点集E 如果存在某一正数r 使得 EU(O r) 其中O是坐标原点 则称E为有界点集 ◆无界集一个集合如果不是有界集 就称这集合为无界集 点集{(x y)| x+y1}是 点集{(x y)| x+y1}是 举例 点集{(x y)|1x 2+y 24} (4)有界集 无界集 是有界闭区域 无界闭区域 无界开区域

4.n维空间* 我们把元有序实数组x1,x2,···,xm)的全体所构成 的集合记为R”,即 Rn=R×R××R={x1,x2,xm)x,∈R,i=1,2,n} x=(x1,x2,·,xn)称为R中的一个点或一个n维向量; x称为点x的第个坐标或n维向量x的第个分量, 0=(0,0,·.·,0称为Rn中的原点或维零向量 HIGH EDUCATION PRESS
我们把n元有序实数组(x1 x2 xn )的全体所构成 的集合记为Rn 即 Rn=RR R={(x1 x2 xn )| xiR i=1 2 n} 4.n维空间* x = (x1 x2 xn )称为Rn中的一个点或一个n维向量 xi称为点x的第i个坐标或n维向量x的第i个分量 0=(0 0 0)称为 Rn 中的原点或n维零向量

4.n维空间 我们把n元有序实数组x,x2,···,x,)的全体所构成 的集合记为R”,即 Rn-R×R××R={x1,x2,.,xnx,∈R,1,2,n} ·线性运算 设x=(1,x2,.,x,y=(y1,2,·,yn)为R0中 任意两个元素,2R,规定 x+y=(x1ty1,x2ty2,··,xn+yn)月 2x=(2x1,2x2,·,2xn) 这样定义了线性运算的集合R"称为n维空间 等HIGH EDUCATION PRESS
我们把n元有序实数组(x1 x2 xn )的全体所构成 的集合记为Rn 即 Rn=RR R={(x1 x2 xn )| xiR i=1 2 n} ◆线性运算 设 x = (x1 x2 xn ) y = (y1 y2 yn ) 为 Rn中 任意两个元素 R 规定 x+y = (x1+y1 x2+y2 xn+yn ) x = (x1 x2 xn ) ◆这样定义了线性运算的集合 Rn 称为 n维空间 4.n维空间*

两点间的距离 >R中点x=(K1,x2,·,xn和点=0y1,2,·,yn间的距离 记作pc,y),规定 p(x,y)=Vx-)2+(x2-2)2++(xn-yn)2 >R中元素x=(x1,x2,··,xn与零元0之间的距离p(化,0) 记作xl,即 xV好+x+.x 注: 在R1、R2、R3中,通常将x记作x: HIGH EDUCATION PRESS
注: ➢ Rn中点x=(x1 x2 xn )和点y=(y1 y2 yn )间的距离 记作(x y) 规定 ◆两点间的距离 2 2 2 2 2 1 1 ( , ) ( ) ( ) ( ) n n x y = x − y + x − y + + x − y ➢ Rn中元素x=(x1 x2 xn )与零元0之间的距离 (x 0) 记作||x|| 即 在R1 、R2 、R3中 通常将||x||记作|x| 2 2 2 2 1 || || n x = x + x + x