
第四节 第十一章 对面积的曲面积分 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算法 考HIGH EDUCATION PRESS 008
第四节 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算法 机动 目录 上页 下页 返回 结束 对面积的曲面积分 第十一章

一、对面积的曲面积分的概念与性质 引例:若曲面Σ是光滑的,它的面密度为连续函数 4(x,Jy,),求它的质量M. 分析:若的密度是均匀的,即4(x,Jy,z)=常数 则 M=u×Σ的面积 而 的面积=∬V1+z径+子 Dxy 其中,:=z(x,y)是曲面的方程 D是Σ在xOy面上的投影。 所谓曲面光滑:曲面上各点处都有切平面,且当点在 曲面上连续移动时,切平面也连续转动, HIGH EDUCATION PRESS
引例: 若曲面 是光滑的, 它的面密度为连续函数 所谓曲面光滑:曲面上各点处都有切平面,且当点在 曲面上连续移动时,切平面也连续转动. 分析:若的密度是均匀的,即 (x, y,z) = 常数 则 M = 的面积 , 而 = + + Dx y x y z z dxdy 2 2 的面积 1 其中,z = z (x , y)是曲面的方程, Dxy 是 在 xOy 面上的投影。 ( x, y,z), 求它的质量 M . 一、对面积的曲面积分的概念与性质
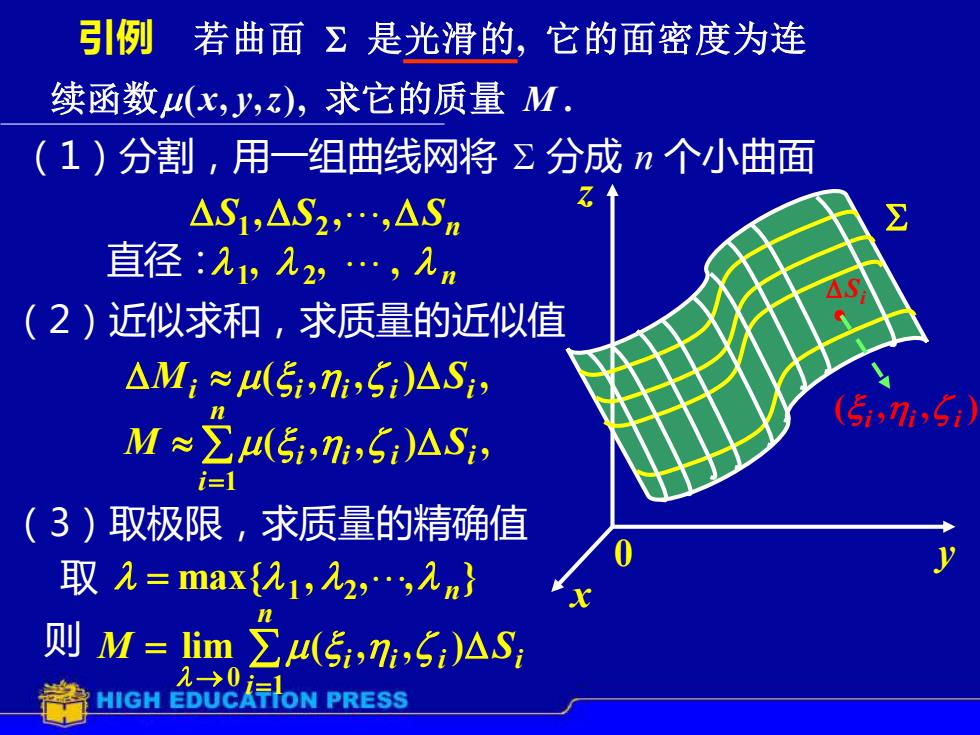
引例 若曲面Σ是光滑的,它的面密度为连 续函数4(x,y,z),求它的质量M. (1)分割,用一组曲线网将Σ分成n个小曲面 △S1,△S2,△Sm 直径1,九2,.,九m △S (2)近似求和,求质量的近似值 △M;≈4(5,n,Si)△Si, M≈∑4(5,7,5i)△S1, i=1 (3)取极限,求质量的精确值 取九=max{21,入2,入m} 则M=1im∑4(5,5i)AS; 入→0 為HIGH EDUC行ON PRESS
若曲面 是光滑的, 它的面密度为连 续函数(x, y,z), 求它的质量 M . 引例 x y z 0 Si (1)分割,用一组曲线网将 分成 n 个小曲面 S S Sn , , , 1 2 直径: n , , , 1 2 (2)近似求和,求质量的近似值 • ( , , ) i i i ( , , ) , Mi i i i Si ( , , ) , 1 = n i M i i i Si (3)取极限,求质量的精确值 max{ , , , } 取 = 1 2 n → = = n i M i i i Si 1 0 lim ( , , ) 则

定义:设Σ为光滑曲面,f(x,y)是定义在∑上的一 个有界函数,若对Σ做任意分割和局部区域任意取点 乘积和式极限 j∬fx,y,=)as k=】 都存在,则称此极限为函数f(x,y)在曲面∑上对面积 的曲面积分或第一类曲面积分其中f(x,?)叫做被积 函数,Σ叫做积分曲面 据此定义,曲面形构件的质量为 M=∬x,x)as 曲面面积为S=∬dS HIGH EDUCATION PRESS 机动目录上页下页返回结束
M = (x, y,z)d S 定义: 设 为光滑曲面, “乘积 和式 极限” 都存在, 的曲面积分 f (x, y,z)d S 其中 f (x, y, z) 叫做被积 据此定义, 曲面形构件的质量为 曲面面积为 f (x, y, z) 是定义在 上的一 个有界函数, 记作 或第一类曲面积分. 若对 做任意分割和局部区域任意取点, 则称此极限为函数 f (x, y, z) 在曲面 上对面积 函数, 叫做积分曲面. 机动 目录 上页 下页 返回 结束

·积分的存在性若f(x,y,z)在光滑曲面∑上连续 则对面积的曲面积分存在 ·对积分域的可加性若Σ是分片光滑的, 例如分成两 片光滑曲面∑1,∑2,则有 Jsfx,yads=3fx,x)ds+八3,fx,)ds 对面积的曲面积分与对弧长的曲线积分性质类似. ·线性性质设k1,飞2为常数,则 不等式性质等 kfx,y,=)±kg(x,y,aS =k1∬fx,y,)ds±k2sg(x,y)ds HIGH EDUCATION PRESS
则对面积的曲面积分存在. • 对积分域的可加性. , , 1 2 则有 = f (x, y,z)d S 1 f (x, y,z)d S k1 f (x, y,z) k2 g(x, y,z) d S • 线性性质. = k1 f (x, y,z)dS k2 g(x, y,z)dS 在光滑曲面 上连续, 对面积的曲面积分与对弧长的曲线积分性质类似. • 积分的存在性. 若 是分片光滑的, 例如分成两 片光滑曲面 不等式性质等