
第四节 第十章 重积分的应用 一、立体体积(已知重积分的应用) 二、 曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力 HIGH EDUCATION PRESS 机动目录上页下页返回结束
第四节 一、立体体积 (已知重积分的应用) 二、曲面的面积 三、物体的质心 四、物体的转动惯量 五、物体的引力 机动 目录 上页 下页 返回 结束 重积分的应用 第十章

一、已知的重积分应用(立体体积) 二重积分 (1)曲顶柱体的体积 V=J∬fx,ydo (2)平面薄片的质量 M=∬4x,y)dc (3)平面区域的面积 S=do 三重积分 (1)空间立体的质量 M=Jj∬px,y) (2)空间立体的体积 HIGH EDUCATION PRESS
一、已知的重积分应用(立体体积) 二重积分 (1)曲顶柱体的体积 (2)平面薄片的质量 三重积分 (1)空间立体的质量 ( , ) D V f x y d = ( , ) D M x y d = (3)平面区域的面积 D S d = M x y z dv ( , , ) = (2)空间立体的体积 V dv =

1.能用重积分解决的实际问题的特点 所求量是 分布在有界闭域上的整体量 对区域具有可加性 2.用重积分解决问题的方法 ·用微元分析法(元素法) 3.解题要点 画出积分域、确定积分序 定出积分限、计算要简便 HIGH EDUCATION PRESS 机动目 录上页下页返回结束
1. 能用重积分解决的实际问题的特点 所求量是 对区域具有可加性 • 用微元分析法 (元素法) 分布在有界闭域上的整体量 3. 解题要点 画出积分域、确定积分序、 定出积分限、计算要简便 2. 用重积分解决问题的方法 机动 目录 上页 下页 返回 结束

定积分的元素法推广到二重积分的应用: 若要计算的某个量U对于xoy面上的闭区域D具有可加 性,即当闭区域D分成许多小闭区域时,所求量相应 地分成许多部分量,且U等于部分量之和。 (1)设想将D分成n个小区域,并任取其一小区域do (2)将相应于小区域dσ的部分量4U近似表达为 △U≈f(x,y)do,则dU=f(x,y)do, (3)U=∬fxy)do 同样,也可将元素法推广到三重积分中。 HIGH EDUCATION PRESS
定积分的元素法推广到二重积分的应用: U f x y d ( , ) , 若要计算的某个量U 对于xoy面上的闭区域D具有可加 性,即当闭区域 D 分成许多小闭区域时,所求量 U相应 地分成许多部分量,且 U 等于部分量之和。 ( , ) D U f x y d = (1)设想将D 分成n 个小区域,并任取其一小区域d (2)将相应于小区域 d 的部分量 U 近似表达为 则 dU f x y d = ( , ) , (3) 同样,也可将元素法推广到三重积分中
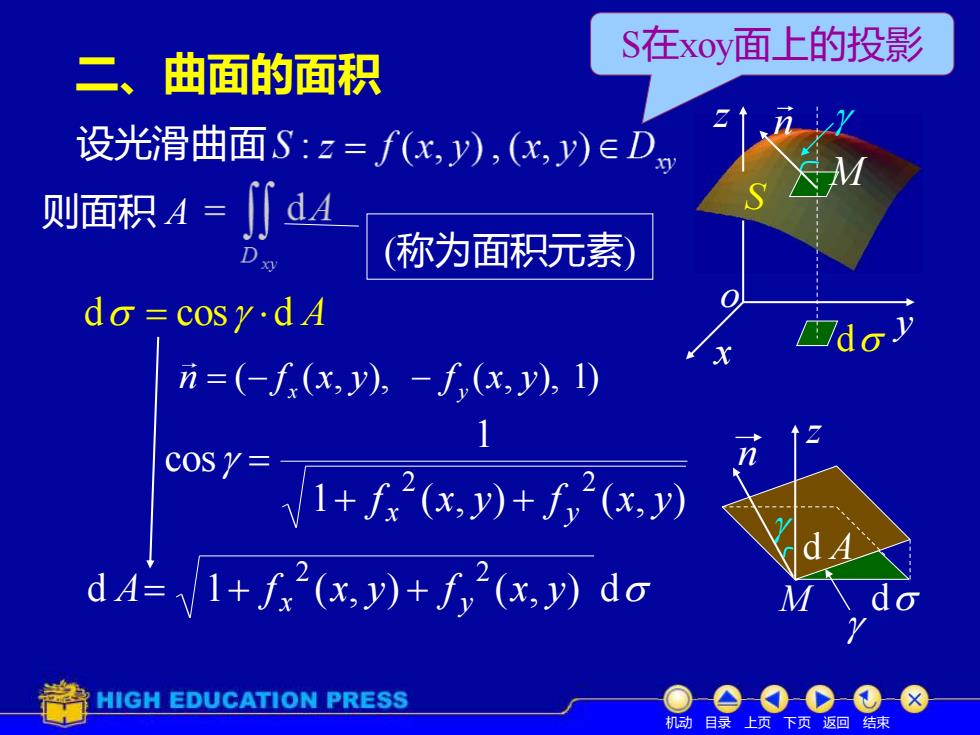
S在xoy面上的投影 二、 曲面的面积 设光滑曲面S:z=f(x,y),(x,y)∈Dg 则面积A三 (称为面积元素) do=cosy.dA do) n=(-∫(x,y),-∫,(x,y),1) o- 1+(x,y)+f2(x,y) dA=1+f2(x,y)+fy2(x,y)do HIGH EDUCATION PRESS 机动目 录上页下页返回结
M d A z d n 二、曲面的面积 x y z S o 设光滑曲面 则面积 A d = cos d A 1 ( , ) ( , ) 1 cos 2 2 f x y f x y + x + y = d 1 ( , ) ( , ) d 2 2 A f x y f x y = + x + y M n d 机动 目录 上页 下页 返回 结束 ( ( , ), ( , ), 1) x y n f x y f x y = − − S在xoy面上的投影 (称为面积元素)