《高等数学》课程教学资源（PPT课件）第十一章_D11_2对坐标曲线积分

第二为 第十一章 对坐标的曲我积分 一、对坐标的曲线积分的概念与性质 二、对坐标的曲线积分的计算法 三、两类曲线积分之间的联系 HIGH EDUCATION PRESS 机动

第二节 一、对坐标的曲线积分的概念与性质 二、 对坐标的曲线积分的计算法 三、两类曲线积分之间的联系 机动 目录 上页 下页 返回 结束 对坐标的曲线积分 第十一章

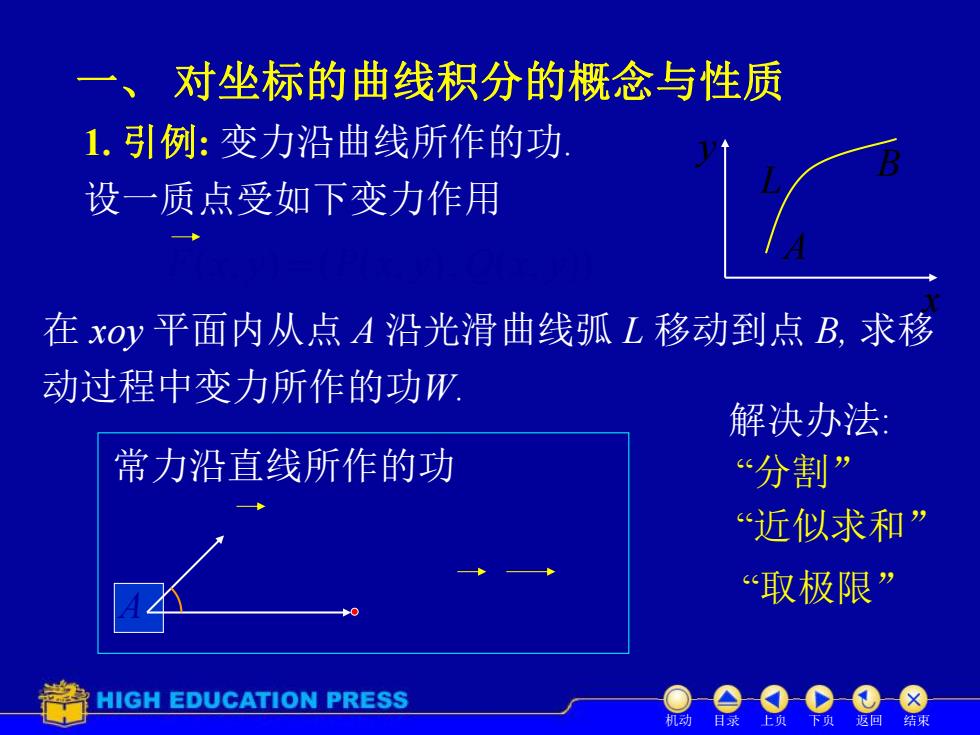
一、对坐标的曲线积分的概念与性质 1.引例：变力沿曲线所作的功 设一质点受如下变力作用 在xOy平面内从点A沿光滑曲线弧L移动到点B,求移 动过程中变力所作的功W 解决办法： 常力沿直线所作的功 “分割” “近似求和” “取极限” HIGH EDUCATION PRESS

一、 对坐标的曲线积分的概念与性质 1. 引例: 变力沿曲线所作的功. 设一质点受如下变力作用 在 xoy 平面内从点 A 沿光滑曲线弧 L 移动到点 B, A B L x y 求移 W  F AB cos “分割” “近似求和” “取极限” 常力沿直线所作的功 解决办法: 动过程中变力所作的功W.  F  AB A B F  F(x, y)  (P(x, y), Q(x, y)) 机动 目录 上页 下页 返回 结束

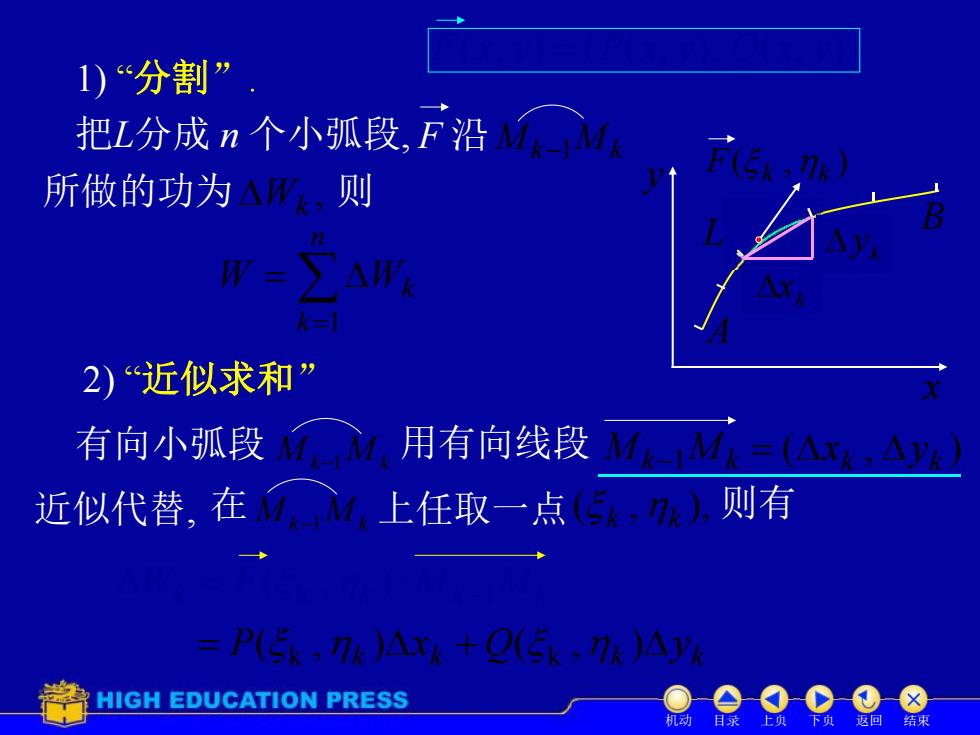
1)“分割” 把L分成n个小弧段，F沿M-M 所做的功为△，则 AW 2)近似求和” 有向小弧段 用有向线段 MM=(AXK.AYK) 近似代替，在M1上任取一点(5，)则有 =P(5k.nk)Axk +Q(5k nk )Ay HIGH EDUCATION PRESS 机动

Mk1 Mk A B x y 1) “分割”. 2) “近似求和” L 把L分成 n 个小弧段, 有向小弧段 M k1M k ( , ) k k  x y 近似代替, ( , ),  k k 则有 k k k k  P( , )x  Q( , )y  k   k  所做的功为 , Wk F 沿Mk1Mk Wk F k Mk 1Mk ( , )       k ( , ) F  k k     n k W Wk 1 则 用有向线段 Mk1Mk 在M k1M k 上任取一点 k y k x 机动 目录 上页 下页 返回 结束 F(x, y)  (P(x, y), Q(x, y))

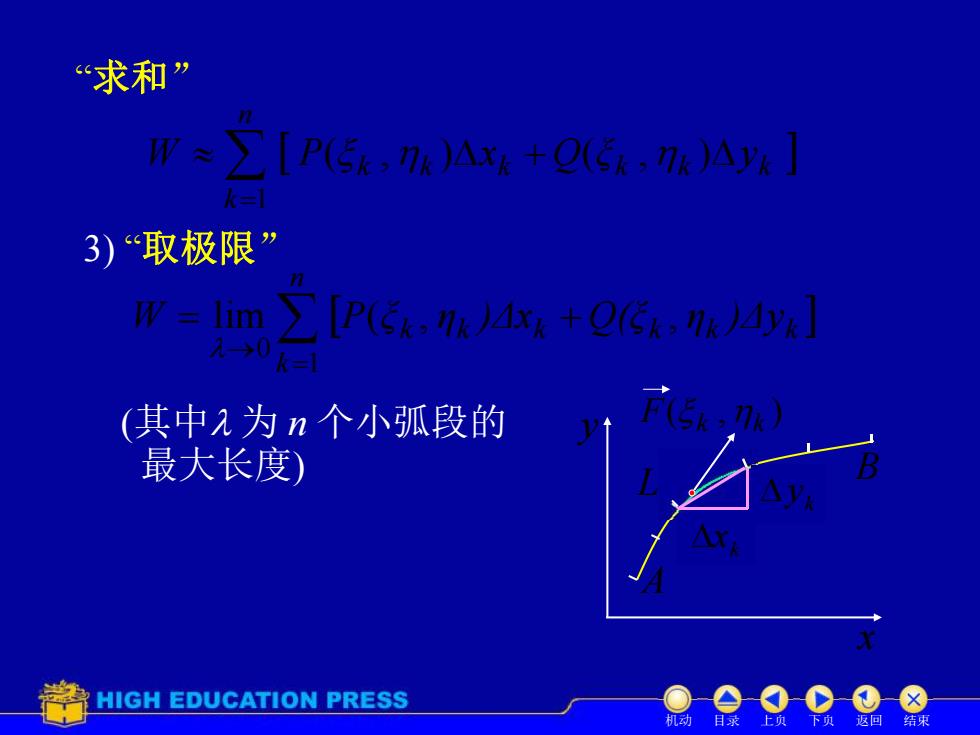
“求和” ∑[P5,Ax+0(:iA] 3)取极限” W=lim P(Ck.K )AXk +Q(CK:K )Ayk k=l (其中入为n个小弧段的 最大长度) HIGH EDUCATION PRESS 目录 返回 结

“求和” 3) “取极限”    n k W 1   k k k k k k P( , )x  Q(ξ , )y     n k W 1 0 lim    k k k k k k P(ξ , η )Δx  Q(ξ , η )Δy Mk1 Mk A B x y L ( , ) F  k k k y k x (其中 为 n 个小弧段的 最大长度) 机动 目录 上页 下页 返回 结束

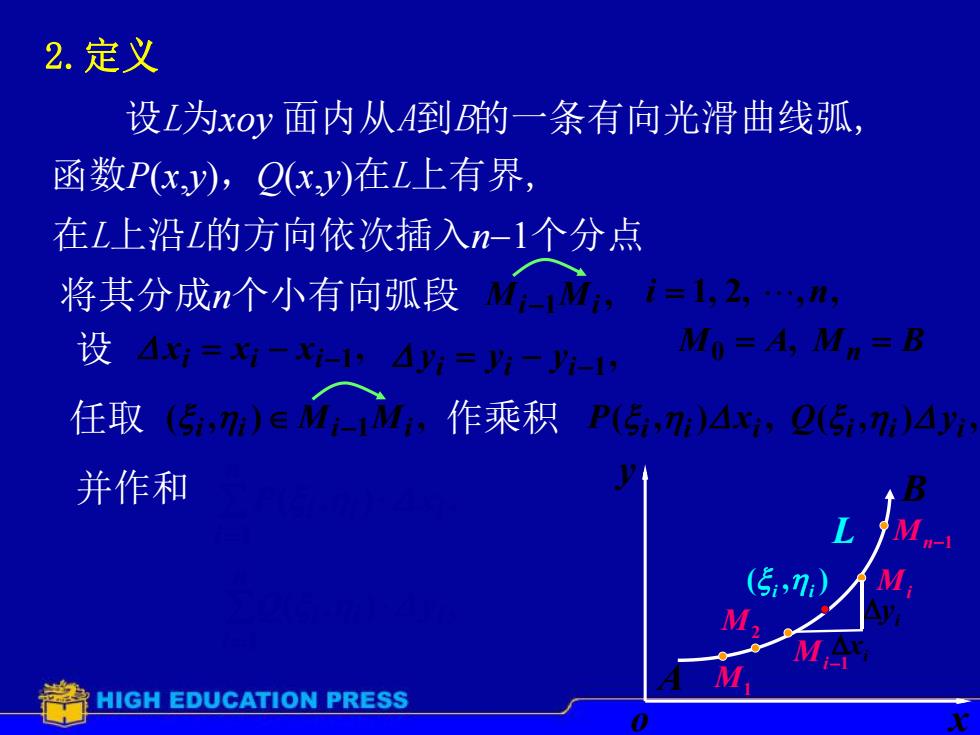
2.定义 设L为xoy面内从A到B的一条有向光滑曲线弧 函数Pxy,Q(xy)在L上有界， 在L上沿L的方向依次插入n-1个分点 将其分成n个小有向弧段-M ,i=1,2、4 设 4=-1:4=片-J-1 Mo=A,Mn=B 任取（传，7）eM 作乘积P(5,)4(,4 并作和 HIGH EDUCATION PRESS

2.定义 设L为xoy 面内从A到B的一条有向光滑曲线弧, 函数P(x,y)，Q(x,y)在L上有界, 将其分成n个小有向弧段 , Mi1Mi o x y A B Mn1 Mi Mi1 M2 M1 ( , ) i i  L 任取 ( , ) ,  i i  Mi1Mi 作乘积 ( , ) , i i i P    x 在L上沿L的方向依次插入n1个分点 i  1, 2, ,n, 设 , M0  A, Mn  B i  i  i1  x x x , i  i  i1  y y y ( , ) , i i i Q    y xi i y 并作和 ( , ) , 1 i n i  P  i i  x  ( , ) , 1 i n i i i Q     y 