
第三节 第十一章 格林公式及其应用 格林公式 二、平面上曲线积分与路径无关的 等价条件 三、二元函数的全微分求积 HIGH EDUCATION PRESS 下页返回结束
第三节 一、格林公式 二、平面上曲线积分与路径无关的 等价条件 机动 目录 上页 下页 返回 结束 格林公式及其应用 第十一章 三、二元函数的全微分求积

问题的提出 牛顿-莱布尼茨公式 ∫Bf(x)k=F(b)-F(a 意义:定积分可通过其原函数在 区间端点上的函数值来表达 问题:二重积分 f∬f(x,y)dxdy 能否表达为某个函数在D的边界 曲线L上的曲线积分? HIGH EDUCATION PRESS
问题的提出 f ( x)dx F(b) F(a) b a 牛顿-莱布尼茨公式 = − 定积分可通过其原函数在 区间端点上的函数值来表达 x y 0 D L ( , ) d d D f x y x y 问题:二重积分 能否表达为某个函数在D的边界 曲线L上的曲线积分? 意义:
预备知识-区域连通性的分类: 设D为平面区域,如果D内任一闭曲线所围成的 部分都属于D,则称D为平面单连通区域,否则称为 复连通区域 单连通区域 复连通区域 复连通区域 单连通区域(无“洞”区域) 区域D分类 多连通区域(有”洞”、点洞区域) HIGH EDUCATION PRESS
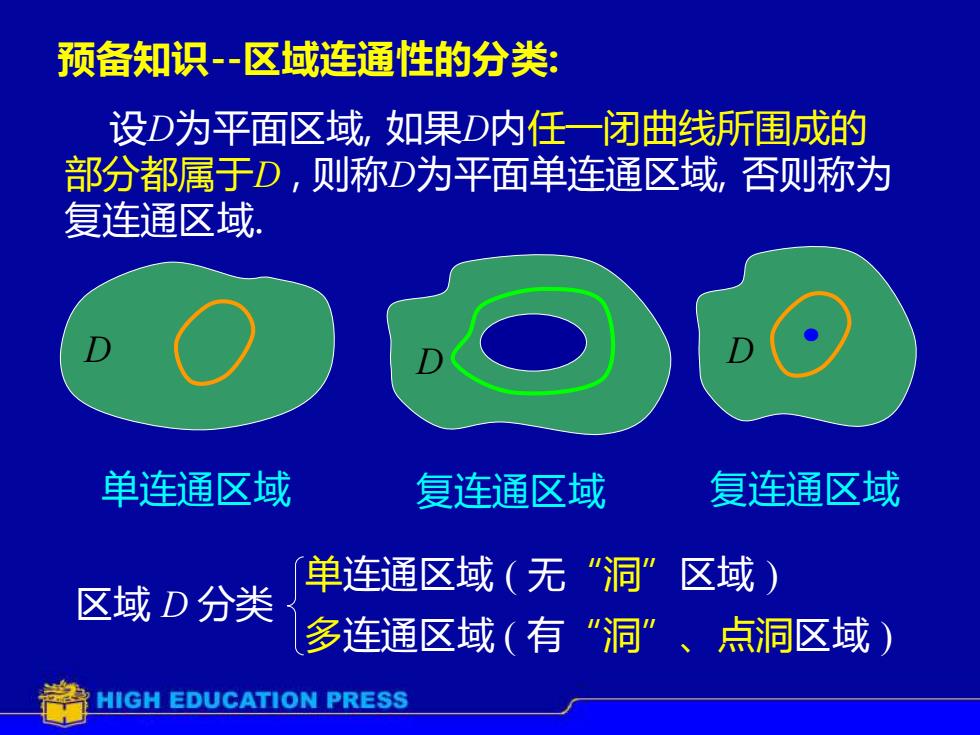
设D为平面区域, 如果D内任一闭曲线所围成的 部分都属于D , 则称D为平面单连通区域, 否则称为 复连通区域. 单连通区域 复连通区域 D D 预备知识-区域连通性的分类: • D 复连通区域 区域 D 分类 单连通区域 ( 无“洞”区域 ) 多连通区域 ( 有“洞”、点洞区域 )

预备知识-·域D边界L的正向 当观察者在L上行走时 D内在他近处的部分总在他的左边。 >外边界的正向是逆时针 内边界的正向是顺时针 HIGH EDUCATION PRESS
L D 当观察者在 L 上行走时, D 内在他近处的部分总在他的左边。 域 D 边界L 的正向 ➢ 外边界的正向是逆时针 ➢ 内边界的正向是顺时针 预备知识-

格林公式 定理1.设闭区域D是由分段光滑正向曲线L围成, 函数P(x,y),Q(x,y)在D上具有连续一阶偏导数 则有 八g-号ad=frs+0,(*, HIGH EDUCATION PRESS
定理1. 设闭区域 D 是由分段光滑正向曲线 L 围成, 则有 = + − D L x y P x Q y y P x Q d d d d ( 格林公式 ) 函数 在 D 上具有连续一阶偏导数, 一、 格林公式