
得到同解方程组 x1+x2-3x3=-1, 一x:十4x3=5, xs=1, 0=1. 所以原方程组无解。 (3》解:对原方程组作初等变换 211 13 1 13 1 5 1 2 115-7 -7 23-314 2 -3 14 f131 5) 3 1 51 0-5-1 -8 1 6 0-2 4-12 1 8 0-3-5 3 -4 131 3 6) 01-2 6 -2 6 0011-22 0 1-2 (00 11-22 0 0 0 得到同解方程组 〔x1十3x2十xg=5, x2一2x3=6, x3=-2. 因此原方程组有唯一解,解为(1,2,一2). (4)答:一般解为 6✉
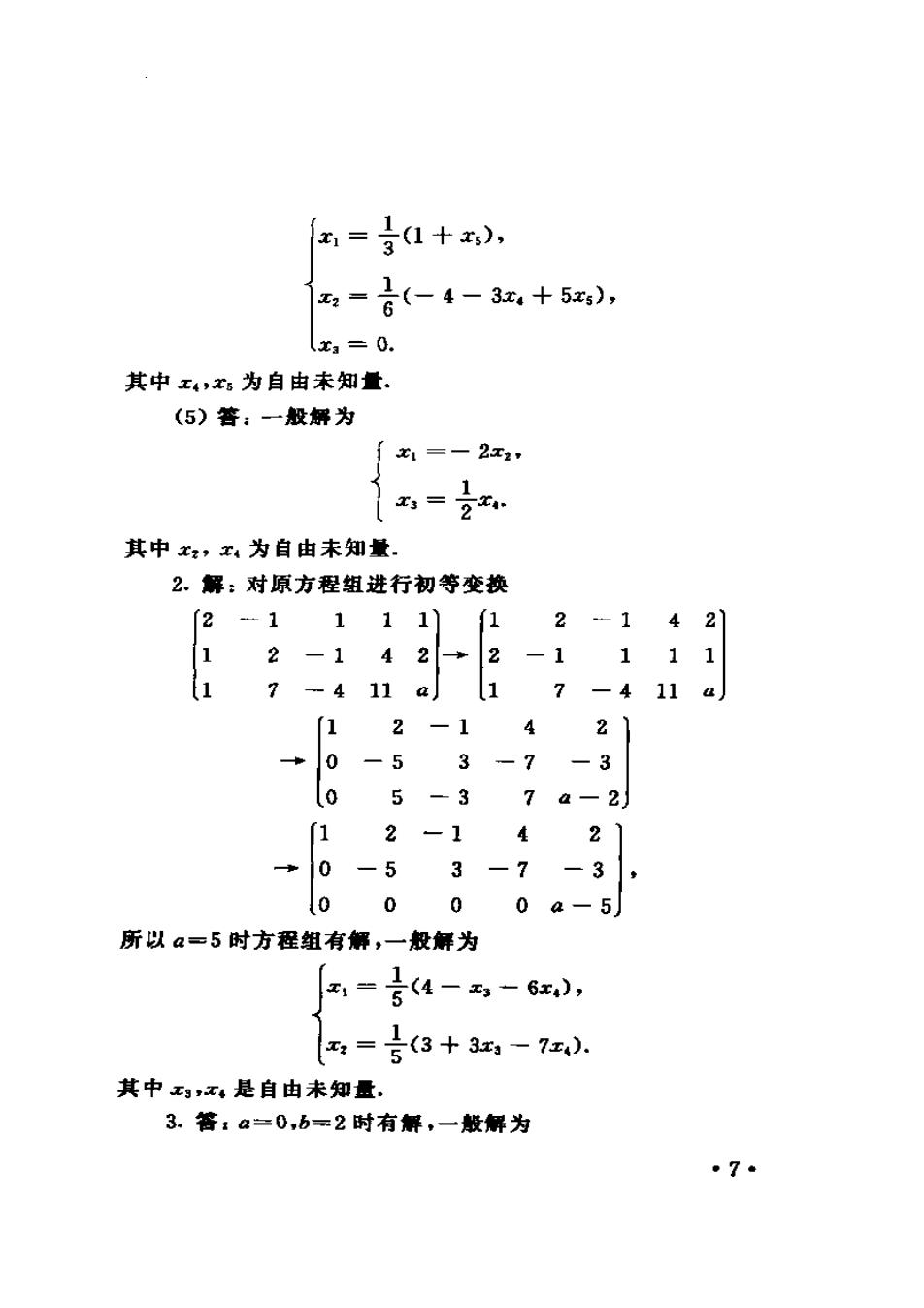
✉=分1+x -合(-4-3+52, (x1=0. 其中x4,x为自由未知量 (5)答:一般解为 「x1=-2x2 x=2x 其中x2,x4为自由未知量. 2、解:对原方程组进行初等变换 2-11111 2-1421 12-142→2-1111 (17-411a17-411a 12-1421 +0-53-7-3 05-37a-2 12-1421 →0-53-7-3] 6 0 00a-5 所以a=5时方程组有解,一般解为 ✉=3(4-,-6x, ✉=号3+3-7x). 其中x,x4是自由未知量. 3.答:a=0,b=2时有解,一般解为 ·7
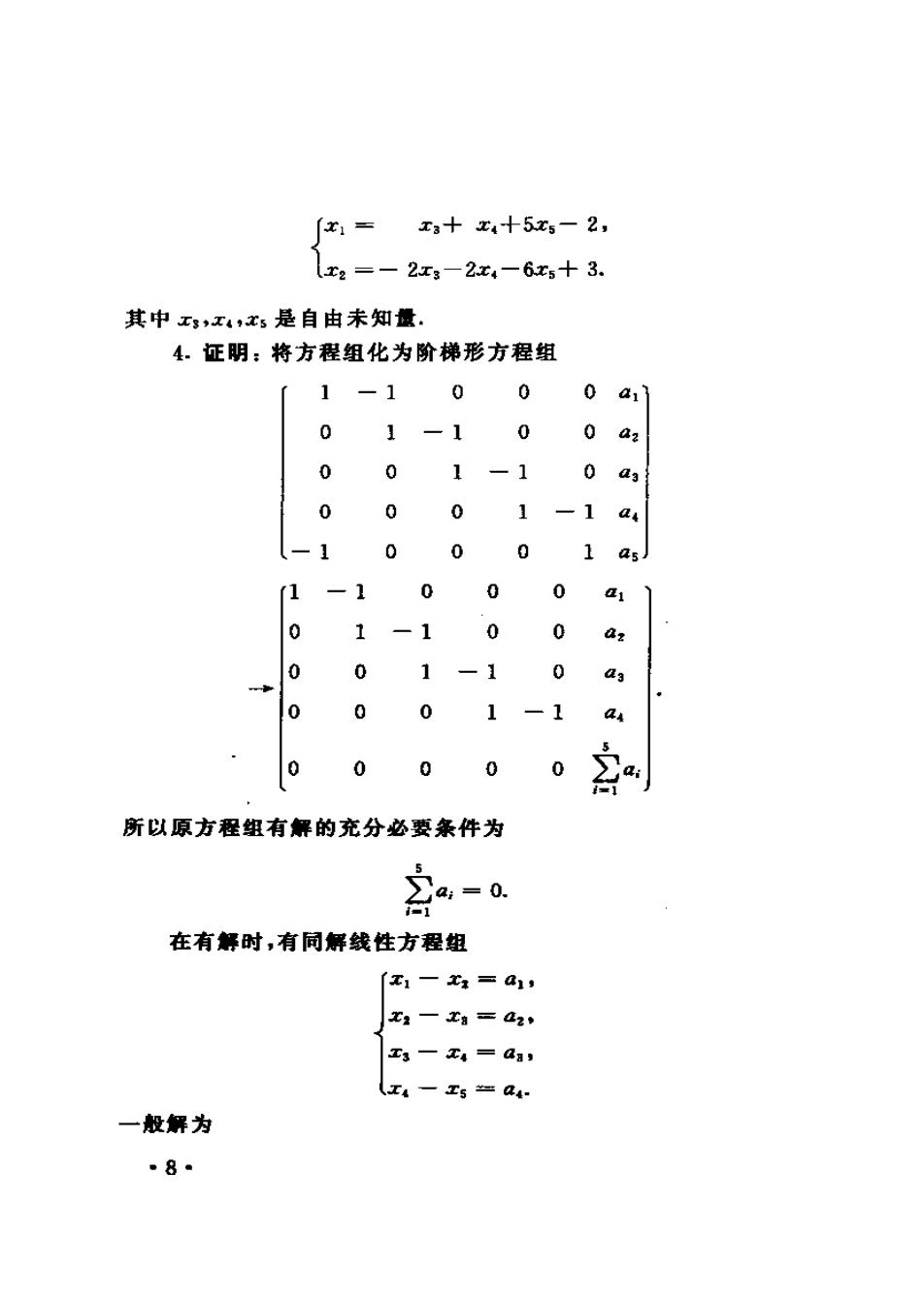
x= xa+x4+5x-2, x2=-2x3-2x4-6x5+3. 其中x,x4,x5是自由未知量. 4.证明:将方程组化为阶梯形方程组 1-1000a1 01-100a2 0 01-10a 0001-14 (-100 01a5 1 -1 000 a 0 1-10 0 0 0 1 -1 0 ag 0 0 0 1-1 0 0 0 0 所以原方程组有解的充分必要条件为 会-a 在有解时,有同解线性方程组 x1-=a, x一xa=a2, 工3-x4=aa, (x4一x5=a4: 一般解为 8

x=a1十a2十as+a4十x3, x2=a2十ag十a4十xs, x4=as十a4十x6, (x4=a4十xs 其中x⅓是自由未知量. 1.2线性方程组的矩阵 内喜捕要 定义2由5X个数排成的5行n列的表 ama1aa】 aaaa2 an 称为一个sXm矩阵。 矩阵中的数a称为矩阵的元素,其中第上个下标表示这个 元素位于矩阵中第行,第2个下标方表示这个元素位于第列. 用大写拉丁字母A,B.(a),(6).表示矩阵.有时候为了 指明A或(a)是一个s义n矩阵,把它表成A或(a).如果矩阵 A的行数与列数相等,都等于n,就称A是一个n阶矩阵或n阶方 阵,简称方阵。 两个矩阵只有当它们的行、列数分别相等,并且对应的元素都 相等时,才称为相等.即相等的矩阵是完全一样的。 定义3矩阵的初等行变换是指下列3种变换: (1)用一个非零的数乘矩阵的某一行. (2)把矩阵的某一行乘k后加到另一行上,k是任意数. (3)互换矩阵中两行的位置. 9

任一个矩阵都可以经过一系列的初等行变换,变成阶梯形矩 阵.所谓阶梯形矩阵是指形如 0121)1-210-1)102 000-1,00120,01-1 l0000}(00032{003 的矩阵.即满足下列条件的矩阵A称为阶梯形矩阵: (1)A的非零行都在上面,零行都在下方. (2)设A有r个非零行,第(i=1,2,“,r)行的首元(非零行 中第一个非零元)所在的列为:,则 i<j<.<i. 阶梯形矩阵简称梯阵.如果梯阵A还满足 (3)A的每个首元都等于1. (4)每个首元所在的列除首元外,其他元素都等于零,那么A 就称为一个约化阶佛形矩阵.简称的化梯阵. 每个矩阵都可经初等行变换化为梯阵,也可经初等行变换化 为约化梯阵.而且矩阵的约化梯阵是唯一的, 定义4矩阵A经过初等行变换化为阶梯形矩阵后,阶梯形 矩阵中非零行的个数称为矩阵A的秩,记作r(A). 元素全等于0的矩阵称为零矩阵,用0表示零矩阵,零矩阵的 秩规定为0,即r(0)=0. 给定一个线性方程组 a1x1十a1x2十十a1xn=b1, a2x1十a2x2十.十anx.=b2, (1) anx1+axzx+.+aaxm=b 把系数按原来的位置写成一个s义n矩阵 ·10-