
2.4矩阵的秩 一、 矩阵的行(列秩、秩 矩阵秩与向量组的极 大 无关组、秩的求法 三、矩阵秩的第二定义 四、小结
§2.4 矩阵的秩 一、 矩阵的行(列)秩、秩 三、矩阵秩的第二定义 四、小结 二、 矩阵秩与向量组的极 大 无关组、秩的求法
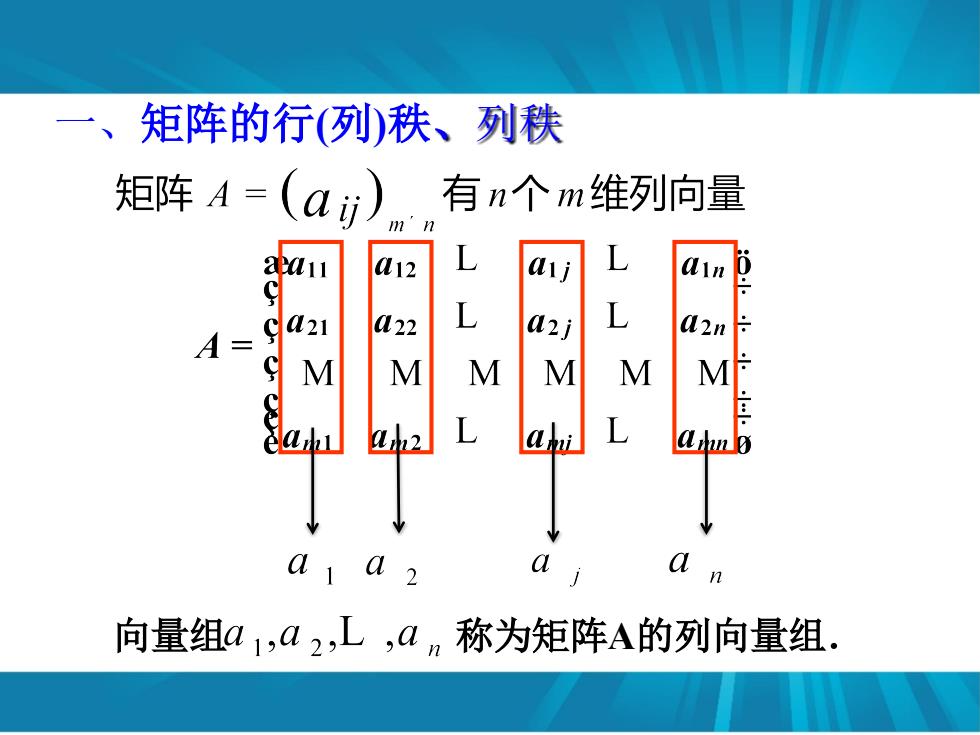
矩阵的行(列秩、列秩 矩阵A=(ai) 有n个m维列向量 u12 L arj a21 M2 L L A= M M M M M M L L 向量组a1,a2,L,a2称为矩阵A的列向量组
一、矩阵的行(列)秩、列秩 向量组 称为矩阵A的列向量组.
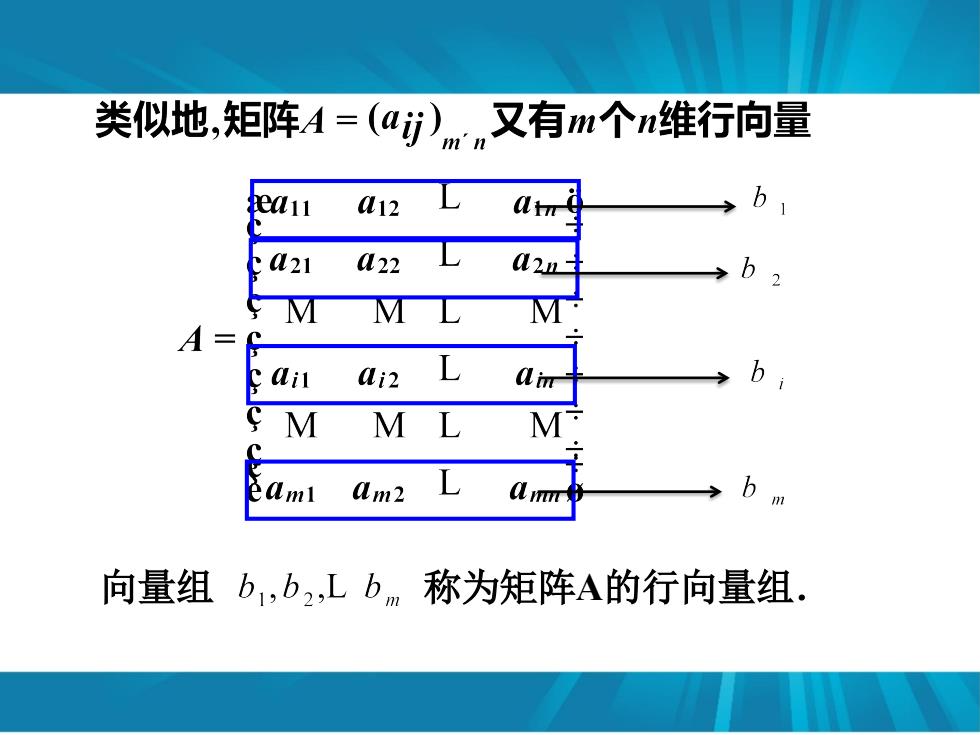
类{似地,矩阵A=(aj)mn又有m个维行向量 ea11 M12 421 M22 S M M M A= cail 4i2 M M M am2 L m 向量组b1,b2,Lb称为矩阵A的行向量组
向量组 称为矩阵A的行向量组.

1.定义2.4.1设mxn矩阵A,称A的行向量组的秩称 为矩阵A的行秩,列向量组的秩称为矩阵A的列秩 l016 例题1:求矩阵A=012的行秩和列秩 214 8 解:A的行向量a1=(1,0,1),a2=(0,1,2),43=(2,1,4) 101 由行列式012=0,知向量组a1,a2,43线性相关, 21
1.定义2.4.1 设m×n矩阵A,称A 的行向量组的秩称 为矩阵A的行秩,列向量组的秩称为矩阵A的列秩. 解:

又a1,M,线性无关,故a1,a,是A的行向量组的一个 最大无关组,所以矩阵A的行秩等于2. 同样方法可以求出A的列秩等于2. ®l1316 例题2:求矩阵A=c02-14的行秩和列秩. 80005每 解:A的三个行向量为 a1=(1,1,3,1),42=(0,2,-1,4),a3=(0,0,0,5). 去掉A的第三个分量量 ae=(1,1,1),a=(0,2,4),a=(0,0,5)
同样方法可以求出A的列秩等于2. 解:A的三个行向量为 去掉A的第三个分量量