
1,-1,1,..,(-1)"+1,.((-1)"-1}n+(-1)"-1-n+(-1)2'3nn数列的(两种)几何表示法:(1)数列对应着数轴上一个点列可看作一动点在数轴上依次取Xi,X2,,Xn.3 X2 X4XiXn数列可看作自变量为正整数n的函数:xn = f(n)整标函数或下标函数
可看作一动点在数轴上依次取 , , , , . x1 x2 xn 1 x 2 x 3 x 4 x n x 1, 1,1, ,( 1) , ; − − n+1 {( 1) } −1 − n , ; ( 1) , , 3 4 , 2 1 2, 1 n n n− + − } ( 1) { 1 n n n− + − 数列的(两种)几何表示法: 数列可看作自变量为正整数 n的函数: x f (n) n = 整标函数或下标函数 (1)数列对应着数轴上一个点列
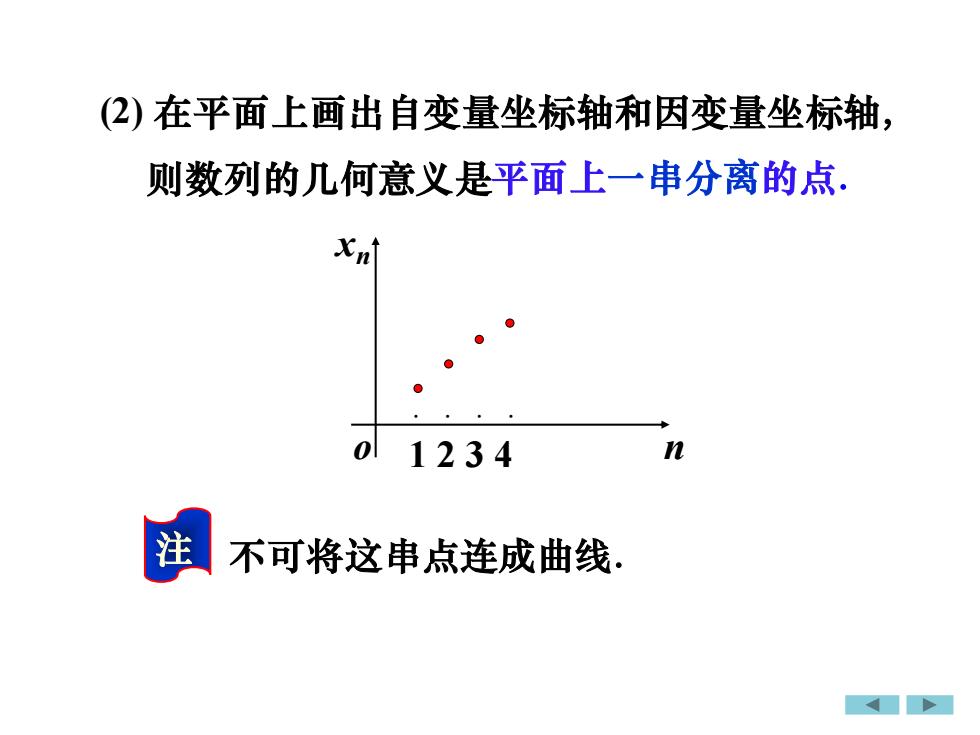
(2)在平面上画出自变量坐标轴和因变量坐标轴则数列的几何意义是平面上一串分离的点xntnD1234注不可将这串点连成曲线
(2) 在平面上画出自变量坐标轴和因变量坐标轴, 注 不可将这串点连成曲线. o n xn · · · · 1 2 3 4 则数列的几何意义是平面上一串分离的点
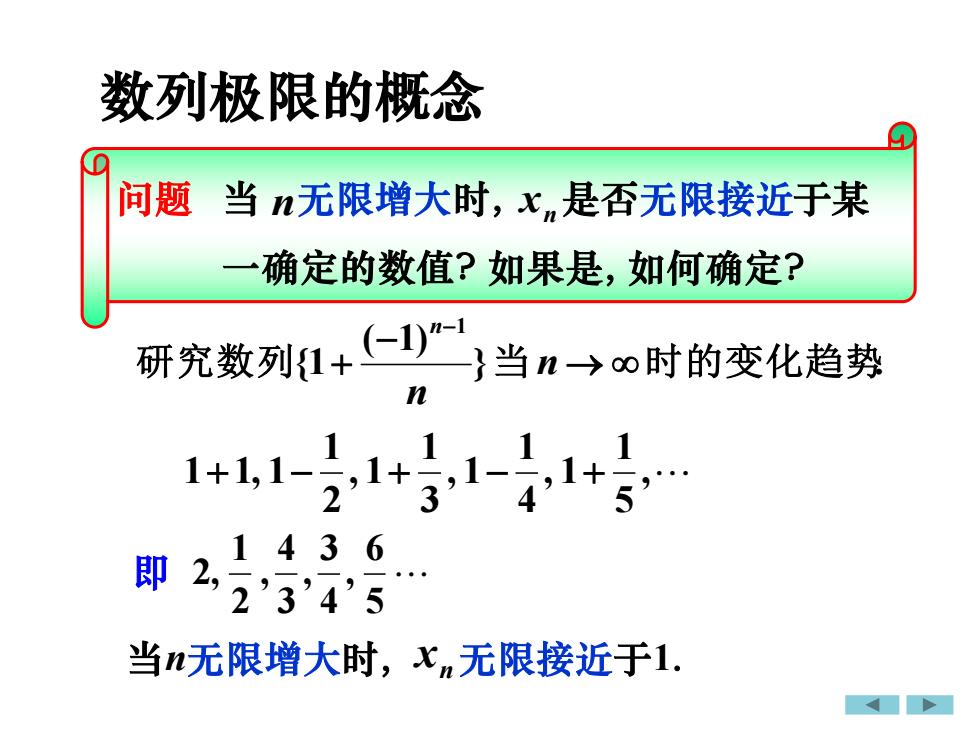
数列极限的概念福问题当n无限增大时,x,是否无限接近于某一确定的数值?如果是,如何确定?(-1)"-1研究数列(11当n→8时的变化趋势n2436即3当n无限增大时,xn无限接近于1
数列极限的概念 } . ( 1) {1 1 研究数列 当 → 时的变化趋势 − + − n n n 即 , 5 1 , 1 4 1 , 1 3 1 , 1 2 1 1+1, 1− + − + 5 6 , 4 3 , 3 4 , 2 1 2, 问题 当 无限增大时, 是否无限接近于某 一确定的数值? n n x 如果是, 当n无限增大时, n x 无限接近于1. 如何确定?

(-1) "-1研究数列(11当n→8时的变化趋势+n当n无限增大时,x无限接近于1.“无限接近”意味着什么?如何用数学语言刻划它,x, -1 /=(1+(-1)"-1x,一1可以要多么小就多么小,只要n充分大则要看x,-1小到什么要求
如何用数学语言刻划它. xn −1 ) 1 1 (1 ( 1) 1 = + − − − n n xn −1 可以要多么小就多么小, 则要看 xn −1 “无限接近”意味着什么? | | } . ( 1) {1 1 研究数列 当 → 时的变化趋势 − + − n n n n 1 = 只要n充分大, 小到什么要求. 当n无限增大时, xn 无限接近于1