《线性代数》课程教学资源（PPT讲稿，C）3-1矩阵的运算

依题意 bu C= 12 4b1+ab1+a13b1 21 l22 L23 b31 41b1+22b21+023b31 25×0.5+20×0.2+18×0.7 29.1 24×0.5+16×0.2+27×0.7 34.1 甲公司每月的利润为29.1万元，乙公司的利润为 4.1万元. T由例题可知矩阵A、B、C的元素之间有下列关系 C=AB= ab1+a12b21+a3b31 azibu+azba+axbst

29.1 34.1   =     C = 25 0.5 20 0.2 18 0.7 24 0.5 16 0.2 27 0.7    +  +  =      +  +  甲公司每月的利润为29.1万元，乙公司的利润为 由例题可知矩阵Ａ、Ｂ、Ｃ的元素之间有下列关系 11 11 12 21 13 31 11 21 11 22 21 23 31 21 a b a b a b c C AB a b a b a b c   + +   = = =       + +   11 11 12 21 13 31 21 11 22 21 23 31 a b a b a b a b a b a b   + + =   + +   11 12 13 21 22 23 a a a a a a       11 21 31 b b b           34.1万元. 依题意

定义若A=()x,B=(bg)xn, 规定AB=C=(C)mn 其中g,=4,4,+a4,+.+ab-2by (i=1,2,.,mj=1,2,.,D 注：1)条件左矩阵A的列数等于右矩阵B的行数 2)方法 左行右列法一一矩阵乘积的元素C 等于左矩阵的第行与右矩阵的第列对应元素 乘积的和. 3)结果左行右列一左矩阵A的行数为乘积 C的行数，右矩阵B的列数为乘积C的列数

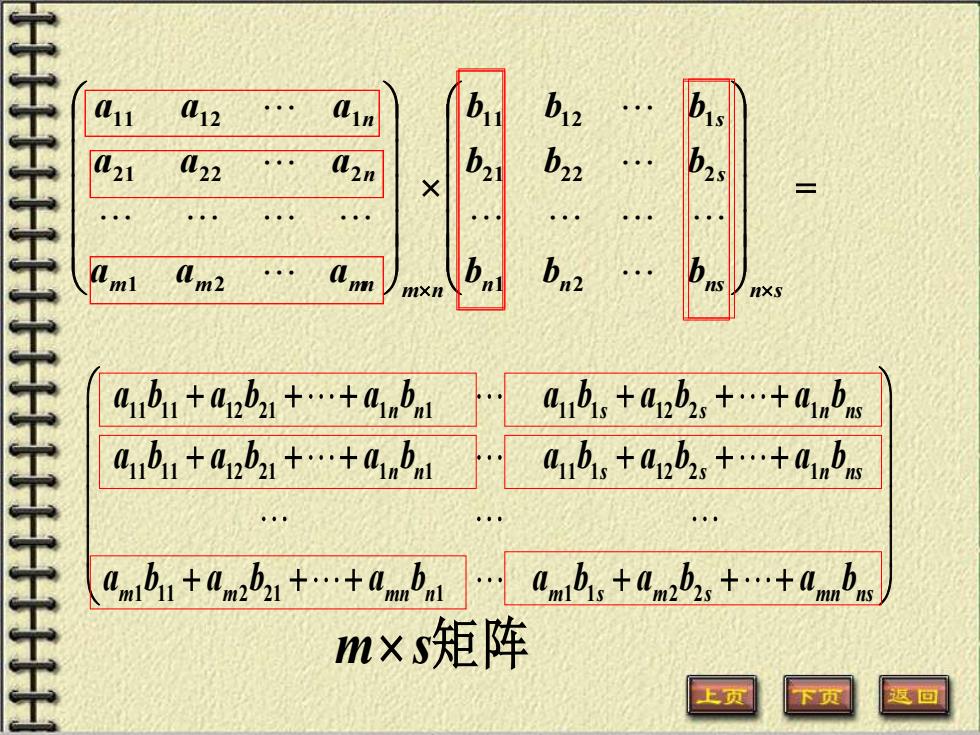
2、定义 ( ) , AB C c = = ij m n ( ) ( ) , 若 A a B b = = ij m n   s s ， ij 规定 1 1 2 2 1 ij i j i j is sj ik kj c a b a b a b a b = = + + +  ｓ ｋ 其中 ＝ （i m j n = = 1 2 1 2 ， ，； ， ，） 注： 1）条件 左矩阵Ａ的列数等于右矩阵Ｂ的行数 2）方法 C ij c 等于左矩阵 的第 行与右矩阵 的第 列对应元素 左行右列法——矩阵乘积 的元素 A i B j 乘积的和. 3）结果 左行右列——左矩阵Ａ的行数为乘积 Ｃ的行数，右矩阵Ｂ的列数为乘积Ｃ的列数

12 L22 b21 biz Aml Am2 ba2 aubu+aba abis+apbzs++aub ab1+azb1+.+4nbn1 4b,+0b,++01nbm anib+0m2b1t.+0mbi.0nmib,+0nmb++ambs m×s矩阵 上页

m m mn m n n n a a a a a a a a a                       1 2 2 1 2 2 2 1 1 1 2 1 =                n n ns ns s s b b b b b b b b b        1 2 2 1 2 2 2 1 1 1 2 1 11 11 12 21 1 1 11 1 12 2 1 11 11 12 21 1 1 11 1 12 2 1 1 11 2 21 1 1 1 2 2 n n s s n ns n n s s n ns m m mn n m s m s mn ns a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b   + + + + + +   + + + + + +       + + + + + +   m s矩阵

例1 8 2×2 例2 设 、3 (1 0 -1 2 2 A= 1 3 0 B- 3 0 1 5 -1 4 41- -1 2 这回

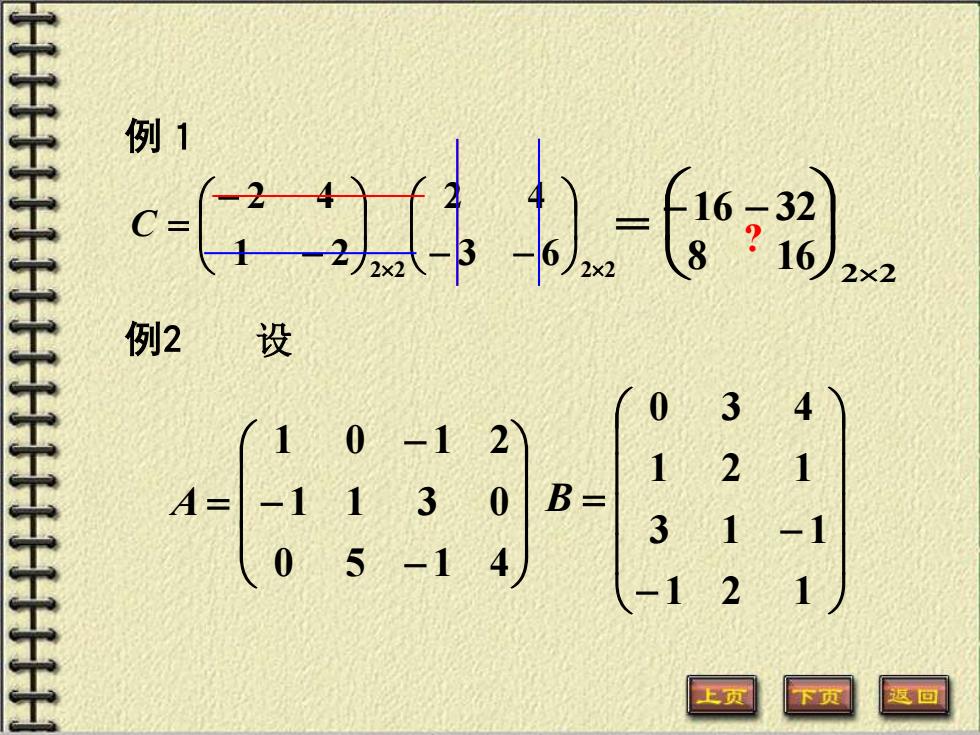
例１ 2 2 2 2 3 6 2 4 1 2 2 4         − −       − − C = 22       = −16 − 32 8 16 设           − − − = 0 5 1 4 1 1 3 0 1 0 1 2 A             − − = 1 2 1 3 1 1 1 2 1 0 3 4 B 例2 ?

解 A=(a与x4,B=bAx .C=(ei 故 C=AB= 05=14 5 6 10 2 -6 217 10

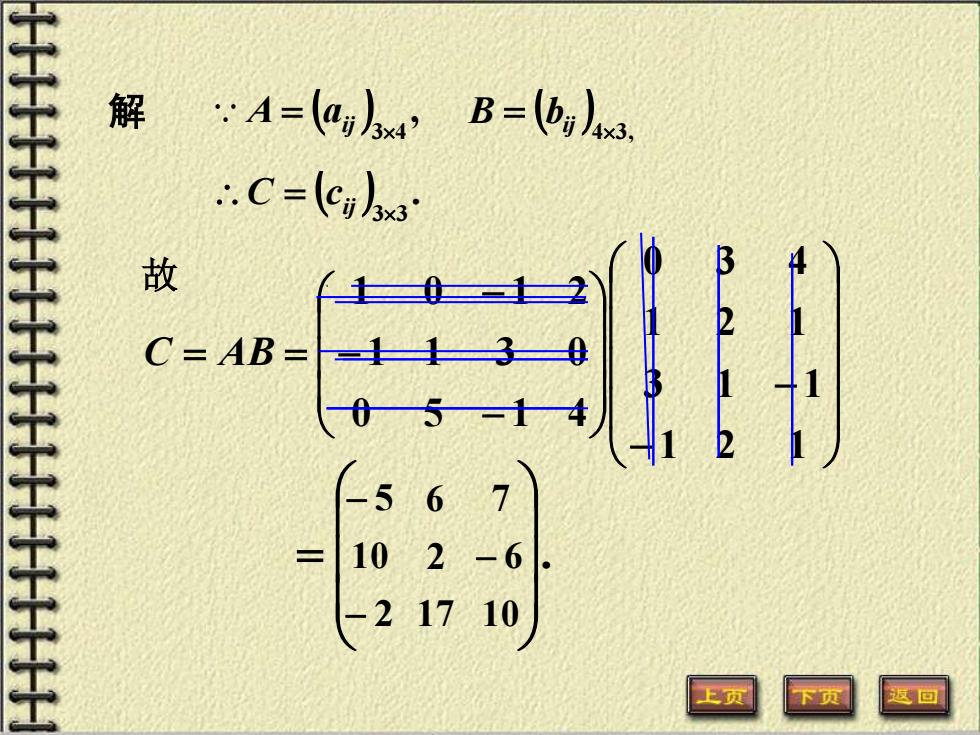
故   − −   − − − = = 1 2 1 3 1 1 1 2 1 0 3 4 0 5 1 4 1 1 3 0 1 0 1 2 C AB .  = 解 ( ) , 34  A = aij ( )4  3 , B = bij ( ) . 33  = ij C c − 5 6 7 10 2 − 6 − 2 17 10