概率论与数理统计 P(X-iY-A-P(Y-jlX-0P(X--a 1 i=1,2,3,4,j≤i. 于是(X,Y)的分布律如下表 XK 1 2 3 4 1 1/4 1/8 1/12 1/16 2 0 1/8 1/12 1/16 3 0 0 1/12 1/16 4 0 0 0 1/16 上一页 下一页 返回
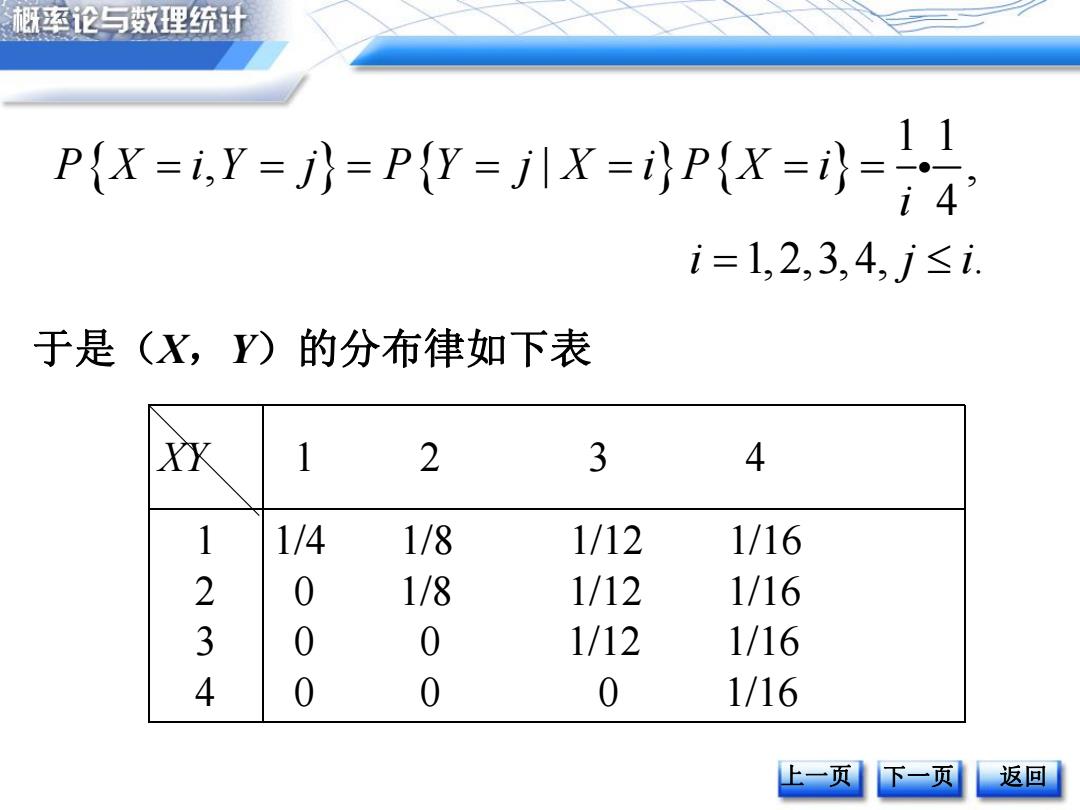
上一页 下一页 返回 于是(X,Y)的分布律如下表 1 1 , | , 4 1,2,3,4, . P X i Y j P Y j X i P X i i i j i XY 1 2 3 4 1 2 3 4 1/4 1/8 1/12 1/16 0 1/8 1/12 1/16 0 0 1/12 1/16 0 0 0 1/16

概率论与数理统计 3、二维连续型随机变量 定义3.4 设(X,)为二维随机向量,X,)的分布函数为 Fc,y).若存在非负二元函数fx,y),对于任意实数xy,有 F(x,Jy)=∫nf(u,v)dd 则侧称(X,Y)为二维连续型随机向量. 非负二元函数f(x,y)称为(X,Y)的 联合概率密度函数,简称为概率密度. 上一页 下一页 返回
上一页 下一页 返回 3 、二维连续型随机变量 , . ( , ) ( , ) 联合概率密度函数 简称为概率密度 非负二元函数 f x y 称为 X Y 的 定义3.4 设(X,Y)为二维随机向量,(X,Y)的分布函数为 F(x,y).若存在非负二元函数f(x,y),对于任意实数x,y,有 x y F ( x, y) f (u, v)dvdu 则称(X,Y )为二维连续型随机向量

概率论与数理统计 概率密度f(x,y)的性质: (1)f(x,y)≥0; (2)["f(u,v)dudy =1 (3)若f(x,y)在(x,y)连续,则 O2F(x,y)=f(x,y) Oxoy (4)设G为xOy平面的一区域,则 P(X,Y)∈G}=Jj丁f(x,y) 上一页 下一页 返回
上一页 下一页 返回 (2) f (u, v)dudv 1 概率密度f ( x, y)的性质: (1) f ( x, y) 0; ( , ) ( , ) (3) ( , ) ( , ) , 2 f x y x y F x y f x y x y 若 在 连续 则 G P X Y G f x y dxdy G xOy {( , ) } ( , ) (4)设 为 平面的一区域 ,则

概率论与数理统计 在几何上z=f(x,y)表示空间的一张曲面. 由性质(2)知, 介于该曲面和xOy平面之间空间区域的体积为1, 由性质(4)知,P{(X,Y)∈D的值等于以G为底, 以曲面z=f(x,y)为顶的曲顶柱体的体积. 上一页 下一页 返回
上一页 下一页 返回 ( , ) . (4) , {( , ) } , 1, (2) , ( , ) . 以曲面 为顶的曲顶柱体的体积 由性质 知 的值等于以 为底 介于该曲面和 平面之间空间区域的体积为 由性质 知 在几何上 表示空间的一张曲面 z f x y P X Y D G xOy z f x y

概率论与数理统计 二维均匀分布 设G是平面上的有界区域,其面积为S,若二维随机变 量(X.,Y)的概率密度为 (x,y)∈G 10 其它 则称X,Y)在区域G上服从均匀分布. 设(X,Y)在区域G上服从均匀分布,D为G内的一区域,即 DcG,且D的面积为SD),那么 PX,)eD-=∬=∬5-S智 S(D) 上一页 下一页 返回
上一页 下一页 返回 设G是平面上的有界区域,其面积为S,若二维随机变 量(X.,Y)的概率密度为 0 其它 ( , ) 1 ( , ) x y G f x y A 设(X,Y)在区域G上服从均匀分布,D为G内的一区域,即 DG,且D的面积为S(D),那么 S S D dxdy S P X Y D f x y dxdy D D 1 ( ) {( , ) ) ( , ) 二维均匀分布 则称(X,Y)在区域G上服从均匀分布