留数计算 Rule:若z为函数f(a)的一级极点,则 Res[f(=),]=lim(-z0)f() m=1 Rule I:若z为函数fa)的m级极点,则 Be/--(- f(z)=Cm(z-2o))m+…+c1(2-)尸+co+C(2-2o)+…+Cn(2-o)”+… (2-2)"fz)=Cm+…+C(2-2)1+m+c(2-2)m+C(-)Hm+…+Cn(2-)+m+… (-bie lexu@mail.xidian.edu.cn 矩阵论 11
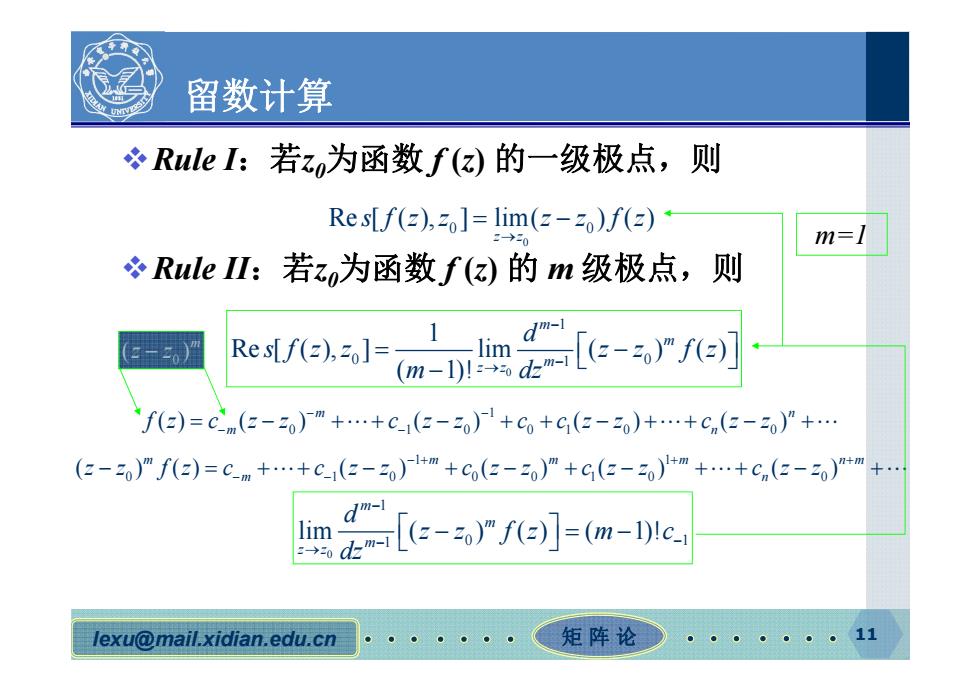
lexu@mail.xidian.edu.cn 矩阵论 11 留数计算 Rule I:若z0为函数 f (z) 的一级极点,则 Rule II:若z0为函数 f (z) 的 m 级极点,则 0 Re [ ( ), ] lim( ) ( ) 0 0 z z s fz z z z fz 0 1 0 0 1 1 Re [ ( ), ] lim ( ) ( ) ( 1)! m m m z z d s fz z z z fz m dz 1 0 1 0 01 0 0 () ( ) ( ) ( ) ( ) m n m n fz c z z c z z c cz z c z z 0 ( )m z z 1 1 0 10 0010 0 ( ) () ( ) ( ) ( ) ( ) m m m m nm m n z z fz c c z z c z z cz z c z z 0 1 1 0 1 lim ( ) ( ) ( 1)! m m m z z d z z fz m c dz m=1

留数计算 Rule III:设f(e)= P() 为Q(口)的一级零点 e() ·P(a)、Qz)在z解析 为Q(2)的一级极点 P(z)0、Q(z0)=0、 2'(z)≠0 则z为函数fd)的一级极点,且Res[f(z),]= P(zo) Q'(z) 11 2()z-z0 p)解析且p不为零 f(z)= 1 g() g回=p(P包)解析且gJ不为零 z-20 P(z) 由Rule n知 Res[f(),zo]=lim(z-z) P()=lim P(=o) 2→z0 Q() →0Q(2)-Q() 2() lexu@mail.xidian.edu.cn ● 矩阵论 12
lexu@mail.xidian.edu.cn 矩阵论 12 留数计算 Rule III:设 P(z)、Q(z)在z0解析 P(z0) ≠0、 Q(z0)=0 、 Q’(z0) ≠ 0 则z0为函数 f (z) 的一级极点,且 ( ) ( ) ( ) P z f z Q z 0 0 0 ( ) Re [ ( ), ] '( ) P z sf z z Q z z0为Q (z) 的一级零点 z0为Q -1(z) 的一级极点 0 1 1 ( ) ( ) z Qz z z φ(z)解析且φ(z0)不为零 0 1 f () () z gz z z g(z)=φ(z)P(z)解析且g(z0)不为零 由Rule I知 0 0 0 0 0 0 0 0 () () ( ) Re [ ( ), ] lim( ) lim zz zz ( ) '( ) () ( ) Pz Pz P z sfz z z z Qz Q z Qz Qz z z