
3.电工技术中遇到的周期函数常具有某种对称性 (1)偶函数纵轴对称,即:f(t)=f(-) (2)奇函数原点对称,即: f(t)=-f(-t) 兴兴光兴 函数的奇偶性与计时起点有关 计时起点的变动→1 )初相改变
3. 电工技术中遇到的周期函数常具有某种对称性 (1) 偶函数纵轴对称,即: f (t) = f (−t) (2) 奇函数原点对称,即: f (t) = − f (−t) ( ) cos ( ) 0 1 = = − a f t k t d t 则 k : 则: ( )sin ( ) 0 1 = = − b f t k t d t k f (t) t − 0 f (t) t − 0 计时起点的变动 f(t)初相改变 **** 函数的奇偶性与计时起点有关 ****

(3)奇谐波函数镜对称,即:∫(t)=-f(t+) 则: f()cos2kmtd(ot)=0 f() b-f()sin2koid()=0 函数的奇谐波性与计时起点无关
(3) 奇谐波函数镜对称,即: ( ) ( ) 2 T f t = − f t + ( ) cos 2 ( ) 0 1 2 = = − a f t k t d t k 则: ( )sin 2 ( ) 0 1 2 = = − b f t k t d t k 函数的奇谐波性与计时起点无关 f (t) t 2 0 T T

4.信号的频谱 (1)幅度频谱 为了表示一个周期函数分解为博氏级数后包含 哪些频率分量和各分量所占的“比重”,常用频谱图 表示。用长度与各次谐波振幅大小相对应的线段,按 频率的高低把它们依次排列起来得到的图形。 (2)相位频谱 把各次谐波的初相用相应的线段依次排列起来得 到的频谱。 由于频率均为基波的整数倍,幅度频谱和相位频谱 均是离散
把各次谐波的初相用相应的线段依次排列起来得 到的频谱。 4. 信号的频谱 为了表示一个周期函数分解为博氏级数后包含 哪些频率分量和各分量所占的“比重”,常用频谱图 表示。用长度与各次谐波振幅大小相对应的线段,按 频率的高低把它们依次排列起来得到 的图形。 (1)幅度频谱 (2)相位频谱 由于频率均为基波的整数倍,幅度频谱和相位频谱 均是离散
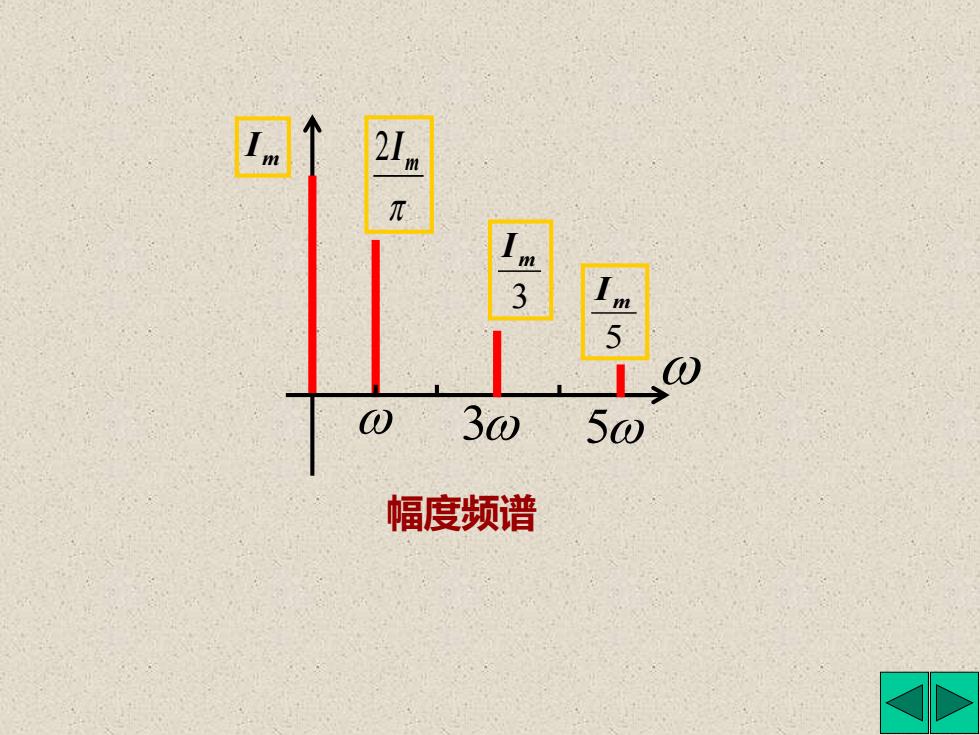
m 30 50 幅度频谱
m 2I 3 m I 3 5 m I 5 幅度频谱 m I
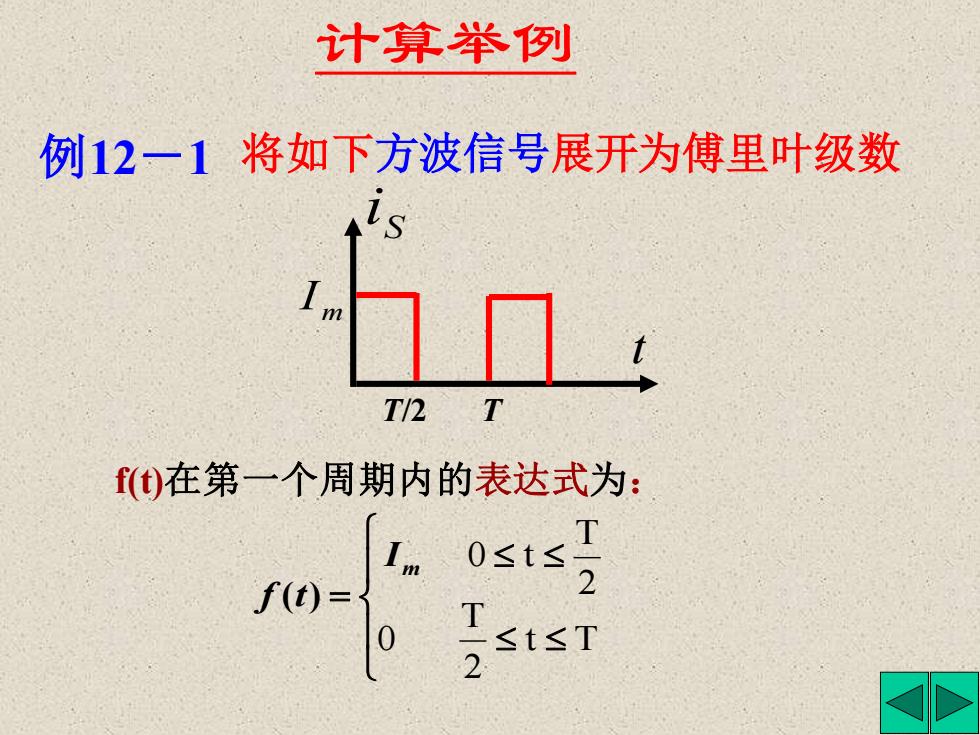
计算举例 例12一1将如下方波信号展开为傅里叶级数 T2 T f0在第一个周期内的表达式为: no- tsT 2
例12-1 将如下方波信号展开为傅里叶级数 t T/2 T S i m I 计算举例 f(t)在第一个周期内的表达式为: = t T 2 T 0 2 T 0 t m I f (t)