《电路》课程教学资源（PPT课件）第12章 非正弦周期电流电路和信号的频谱

3.半波整流电路的输出信号 灯

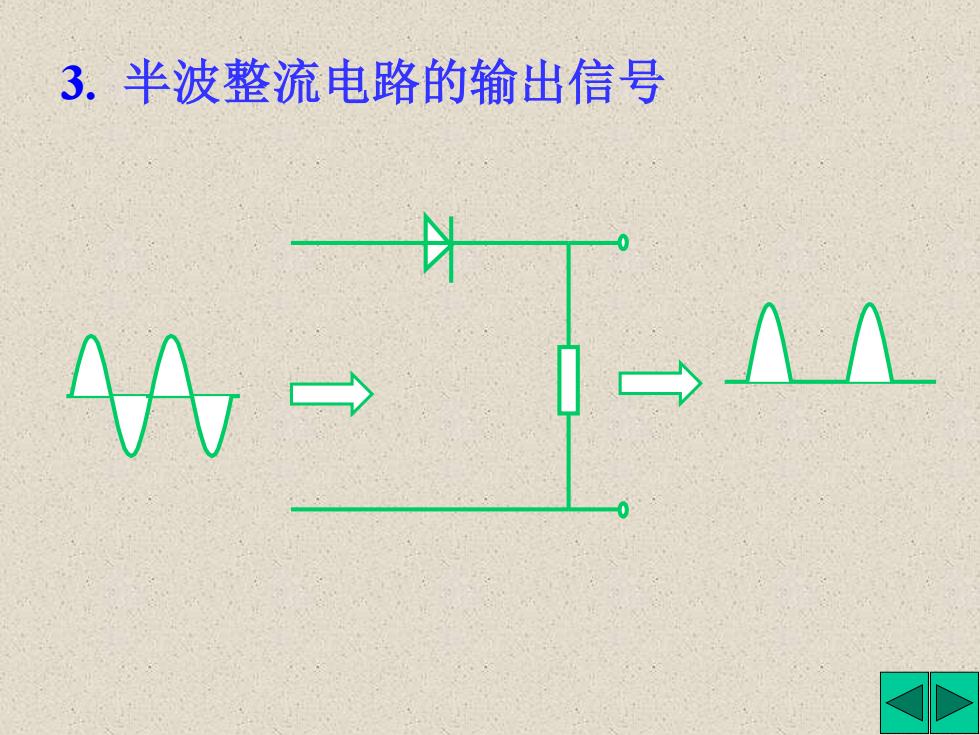
3. 半波整流电路的输出信号

§12.2周期函数的分解 周期函数f(t)=∫(t+kT) 式中T为周期，且k=0,1,2,3. 1.傅里叶级数分解条件： 周期性 连续或只有有限个第一类 间断点（左右极限存在） 狄里赫利条件 只有有限个极值点 电工技术中的周期函数通常都能满足

§12.2 周期函数的分解 周期函数 f（t）＝f（t＋ kT） 式中 T为周期，且 k＝ 0，1，2，3··· 电工技术中的周期函数通常都能满足 1. 傅里叶级数分解条件: 狄里赫利条件 周期性 连续或只有有限个第一类 间断点（左右极限存在） 只有有限个极值点

2.周期函数f(t)如何展开成博里叶级数 f(t)=Ao 直流分量 基波（和原 十A1mc0s(Ot+W1） 函数同频) +A2mc0s(20t+V2】 二次谐波 (2倍频) 高次谐波 =A,+∑A cos((ko+,)三角级数

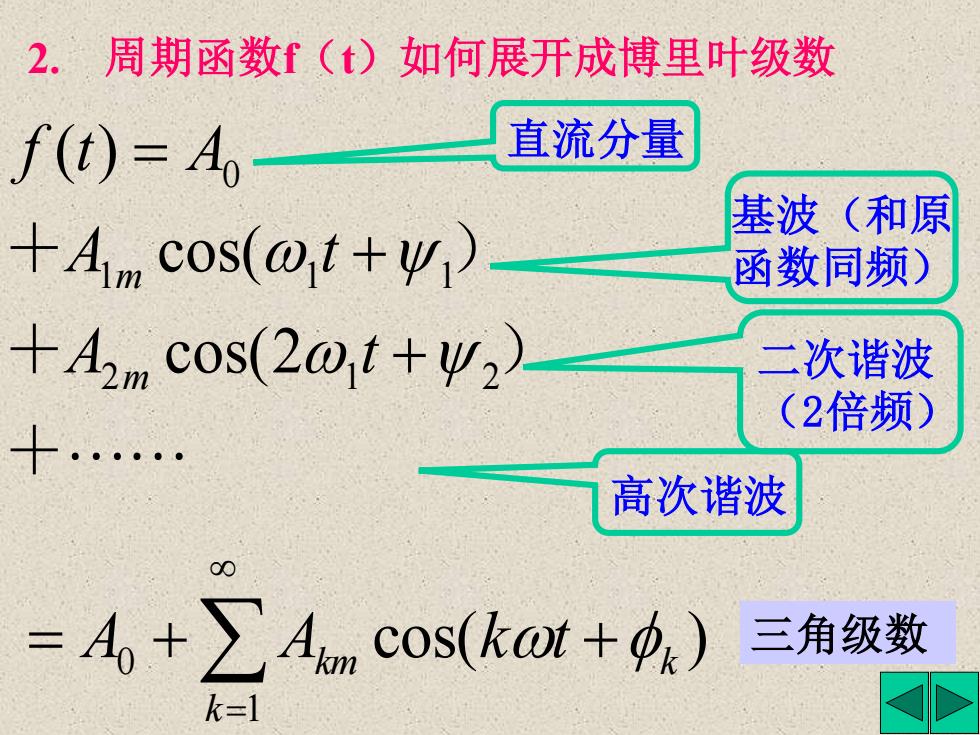
基波（和原 函数同频） 二次谐波 （2倍频） 直流分量 高次谐波 2. 周期函数f（t）如何展开成博里叶级数 cos( ) 三角级数 1 0   = = + + k km k A A kt  ＋ ＋ ） ＋ ） 2 1 2 1 1 1 0 cos(2 cos( ( )     + + = A t A t f t A m m

周期函数 f()=A。+∑dim cos(k0t+ps) 三角级数 Aim cos(kot+) A (coskotcosp-sin kotsin =Akm cosp cos kot-Aim sin or sin kot -ak coskot+b sin kot ax =Ain Cos x br=-Aim sin p f()=4,+∑a:oskot+∑b:sinkot k= k=1

 = = = + + 1 1 0 k k k k f ( t) a a cos k  t b sin k  t 周期函数 ( ) cos( ) k k k m f t = A +  A k  t +  = 1 0 a k t b k t A k t A k t A k t k t A k t k k km k km k km k k km k = + = − = − +            cos sin cos cos sin sin (cos cos sin sin ) cos( ) k Akm k a = cos  k Akm k a 0 = A0 b = − sin  三角级数

谐波分析-把一个周期函数展开或分解为具有 系列谐波的博里叶级数。 00 00 f(t)=a,+∑cosk t+∑b:sinkot k=1 k=1 a,=7f0a0)=7Jf0d0 k= 0 oko-汇k知iW 0=上ko 1 6.-子si)

   =  = = + + 1 1 0 k k k k f ( t) a a cos k t b sink t 谐波分析-把一个周期函数展开或分解为具有 一系列谐波的博里叶级数。 2 2 1 1 0 0 0 0 2 2     = = = = − T k T k T f t k t d t T b f t k t d t T a f t d t T f t d t T a T T ( )sin ( ) ( )cos ( ) ( ) ( ) ( ) ( )   1 1 2 2 0 2 2    − − = = =           ( )cos ( ) ( )cos ( ) ( )cos ( ) f t k t d t f t k t d t f t k t d t T T T