
第五章定积分 高等数学少学时 计。小 dx =典财 解 im [aretanx = lim arctanb 元 b→+00 2 =, dx -lim [arctanx] 元 =lim arctana 1→-00 2 北京邮电大学出版社 06
6 例2 计算 0 2 2 2 0 d d d , , . 1 1 1 x x x x x x + + + + + − − 解 2 2 0 0 d d lim 1 1 b b x x x x + →+ = + + 0 lim arctan b b x →+ = lim arctan a a →− = − 0 0 2 2 d d lim 1 1 a a x x − x x →− = + + 0 lim arctan a a x →− = lim arctan b b →+ = 2 = 2 =
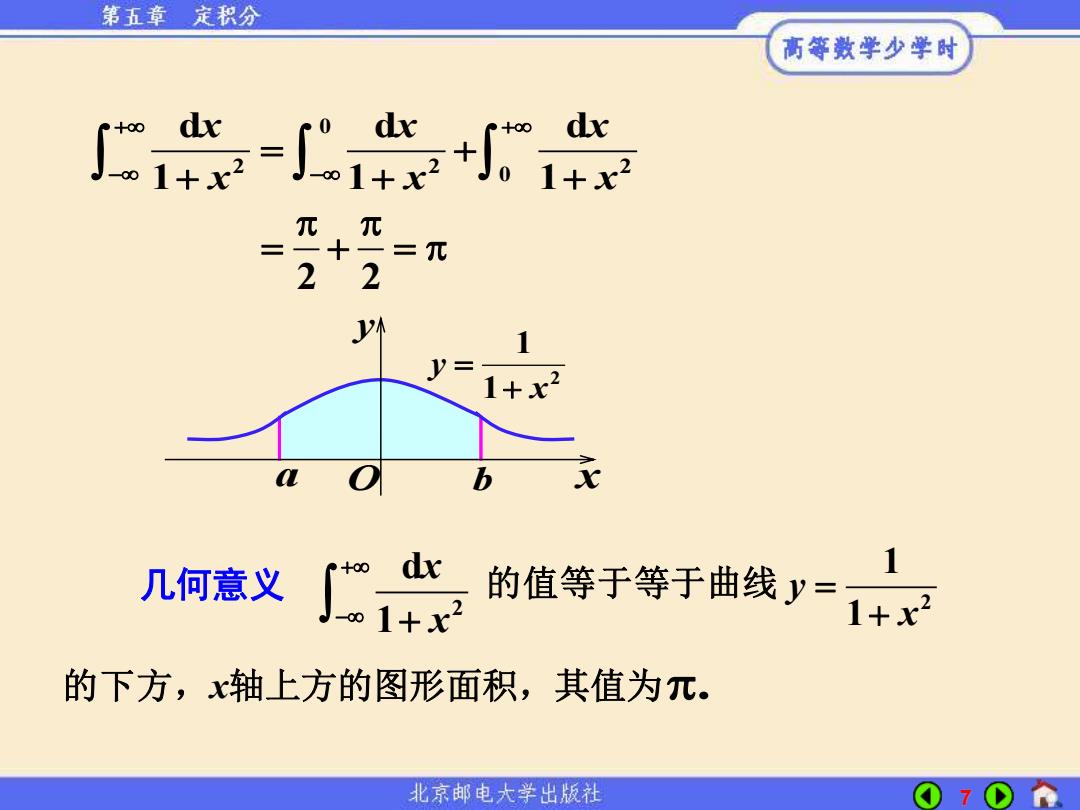
第五章 定积分 高等数学少学时 dx 元 2 2 y= 1+x2 b x 1 几何意义 dx 的值等于等于曲线y= 1+x2 的下方,x轴上方的图形面积,其值为元。 北京邮电大学出版社 7
7 0 2 2 2 0 d d d 1 1 1 x x x x x x + + − − = + + + + 2 2 = + = y a O b x 2 1 1 x y + = . 几何意义 2 d 1 x x + − + 的值等于等于曲线 2 1 1 y x = + 的下方,x轴上方的图形面积,其值为