
§3.3泊松过程(一) 一、计数过程与泊松过程 在天文,地理,物理,生物,通信,医学, 计算机网络,密码学等许多领域,都有关于随 机事件流的计数问题,如: 盖格记数器上的粒子流; 电话交换机上的呼唤流; 计算机网络上的(图象,声音)流; 编码(密码)中的误码流; 电子科技大学
电子科技大学 一、计数过程与泊松过程 在天文,地理,物理,生物,通信,医学, 计算机网络,密码学等许多领域,都有关于随 机事件流的计数问题,如: 盖格记数器上的粒子流; 电话交换机上的呼唤流; 计算机网络上的(图象,声音)流; 编码(密码)中的误码流; §3.3 泊 松 过 程(一)

§3.3泊松过程(一) 交通中事故流; 细胞中染色体的交换次数,… 均构成以时间顺序出现的事件流A1A2,… 定义3.3.1随机过程{N),仑0}称为计数过 程(Counting Process),如果N()表示在(0,)内 事件A出现的总次数 计数过程应满足: (1)W(t)≥0; 电子科技大学
§3.3 泊 松 过 程(一) 电子科技大学 交通中事故流; 细胞中染色体的交换次数,… 均构成以时间顺序出现的事件流 A1 ,A2 , … 定义3.3.1 随机过程{N(t), t≥0}称为计数过 程(Counting Process),如果N(t)表示在(0, t)内 事件A 出现的总次数. 计数过程应满足: (1) N( t )≥0;
§3.3泊松过程(一)》 (2)N(t)取非负整数值; 3)如果s<t,则N(s)≤Nt); (4)对于s<t,N()一NS)表示时间间隔(S,)内 事件出现的次数, 0 Poisson.过程是一类很重要的计数过程. 电子科技大学
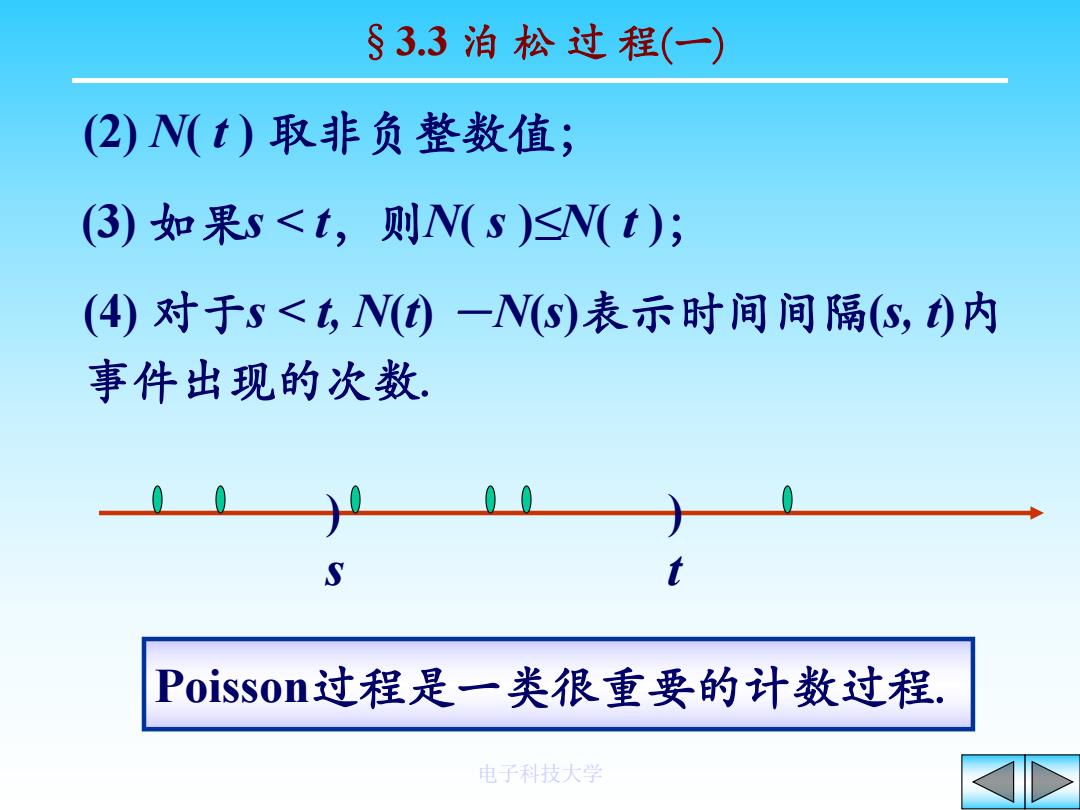
§3.3 泊 松 过 程(一) 电子科技大学 (2) N( t ) 取非负整数值; (3) 如果s < t,则N( s )≤N( t ); (4) 对于s < t, N(t) -N(s)表示时间间隔(s, t)内 事件出现的次数. ) s ) t Poisson过程是一类很重要的计数过程

§3.3泊松过程(一) Poisson过程数学模型: 电话呼叫过程设N(t)为[0,)时间内到达 的呼叫次数,其状态空间为 E={0,1,2,…} 此过程有如下特,点: 1)零初值性N(0)=0; 2)独立增量性任意两个不相重叠的时间间 隔内到达的呼叫次数相互独立; 电子科技大学
§3.3 泊 松 过 程(一) 电子科技大学 Poisson过程数学模型: 电话呼叫过程 设N ( t )为[0, t) 时间内到达 的呼叫次数, 其状态空间为 E={0,1,2,…} 此过程有如下特点: 1) 零初值性 N( 0 )=0; 2) 独立增量性 任意两个不相重叠的时间间 隔内到达的呼叫次数相互独立;

§33泊松过程(一) 3)齐次性在(S,)时间内到达的呼叫次数仅与 时间间隔长度-5有关,而与起始时间无关; 4)普通性在充分小的时间间隔内到达的呼 叫次数最多仅有一次,即对充分小的△t有 P{N(△t)=0}=p(△t)=1-入△t+o(△t), P{N(△t)=1}=p(△t)=入△t+o(△t): P{N(△)≥2}=∑pk(△t)=o(△t), k=2 其中2>0. 电子科技大学
§3.3 泊 松 过 程(一) 电子科技大学 3) 齐次性 在(s, t)时间内到达的呼叫次数仅与 时间间隔长度t-s 有关,而与起始时间 s 无关; 4)普通性 在充分小的时间间隔内到达的呼 叫次数最多仅有一次,即对充分小的Δt,有 { ( ) 0} ( ) 1 ( ), 0 P N t p t t o t { ( ) 1} ( ) ( ), 1 P N t p t t o t { ( ) 2} ( ) ( ), 2 P N t p t o t k k 其中λ>0