
§5.3平稳过程的各态历经性 问题背景 1)在何种条件下,可以依据平稳过程的 一条现实建立有效描述过程的数学模型? 2)实际问题中常需确定随机过程的数学 期望和方差、相关函数; 如飞机在高空飞行,受湍流影响产生机翼 震动,需考虑机翼振幅大小的均值与方差. 电子科技大学
电子科技大学 §5.3 平稳过程的各态历经性 一、问题背景 1)在何种条件下, 可以依据平稳过程的 一条现实建立有效描述过程的数学模型? 2)实际问题中常需确定随机过程的数学 期望和方差、相关函数; 如飞机在高空飞行,受湍流影响产生机翼 震动,需考虑机翼振幅大小的均值与方差

电路中电子不规则运动引起的热噪声(电 位的脉动)考虑脉动范围,噪声功率等归结为 求过程的方差,相关系数 2)对实际动态数据进行零均值化,如何从 数据得到均值函数? 3)困难在于需知道过程的一、二维分布. 4)设想用试验法解决. 电子科技大学
电子科技大学 电路中电子不规则运动引起的热噪声(电 位的脉动).考虑脉动范围,噪声功率等归结为 求过程的方差, 相关系数. 2)对实际动态数据进行零均值化, 如何从 数据得到均值函数? 3)困难在于需知道过程的一、二维分布. 4)设想用试验法解决
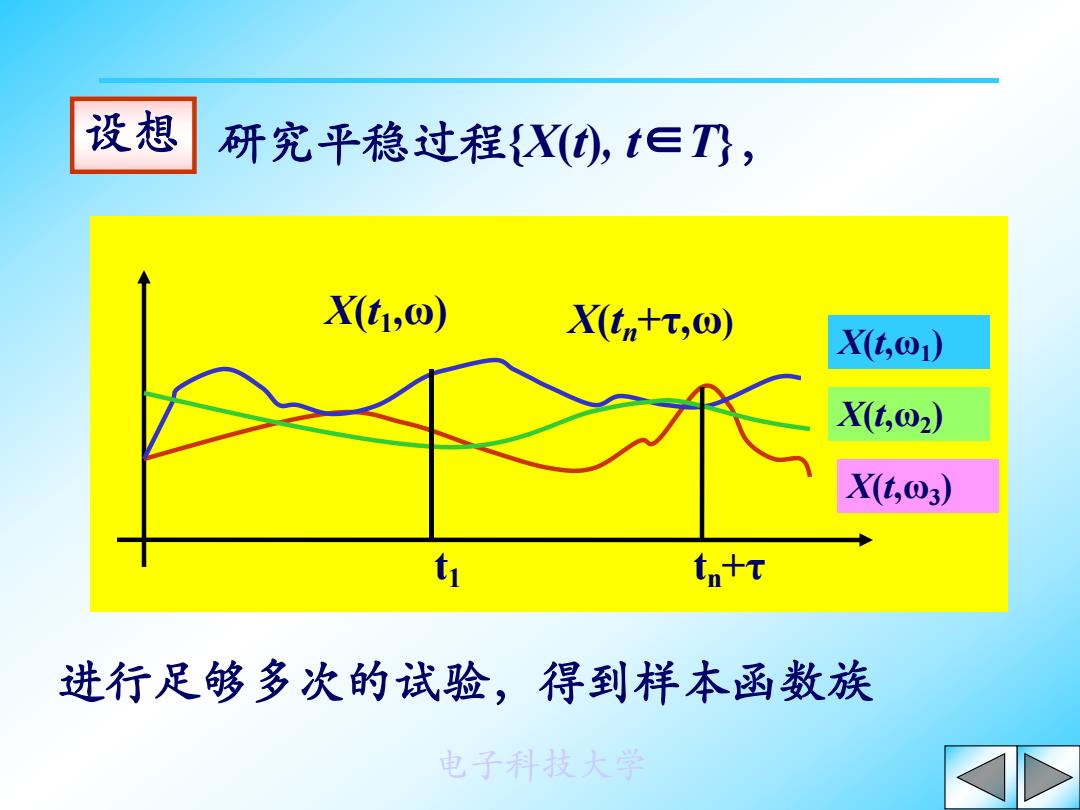
设想 研究平稳过程{X(t),t∈T, X(t1,O) X(tn+t,@) Xt,0) X(t,02) Xt,03) tn+t 进行足够多次的试验,得到样本函数族 电子科技大学
电子科技大学 设想 研究平稳过程{X(t), t∈T}, X(t1 ,ω) X(t,ω1) X(t,ω2) X(t,ω3) t1 tn+τ X(tn+τ,ω) 进行足够多次的试验,得到样本函数族

{(x(t,o1)x(t,o2),…,x(t,⊙n),t∈T} 根据大数定律,对固定t∈T,可令 mx()≈2 nk=1 统计平均 x((e)≈∑)x低+, n k=1 缺,点1)需要很大n,实际工程中难以实现. 2)过程具有不可重复性. 电子科技大学
电子科技大学 {( ( , ), ( , ), , ( , )), } x t 1 x t 2 x t n t T 根据大数定律,对固定t1∈T,可令 ( ), 1 ˆ ( ) 1 1 1 n k X k x t n m t 1 1 1 1 ˆ ( ) ( ) ( ), n X k k k R x t x t n 缺点 1) 需要很大 n ,实际工程中难以实现. 统计平均 2) 过程具有不可重复性
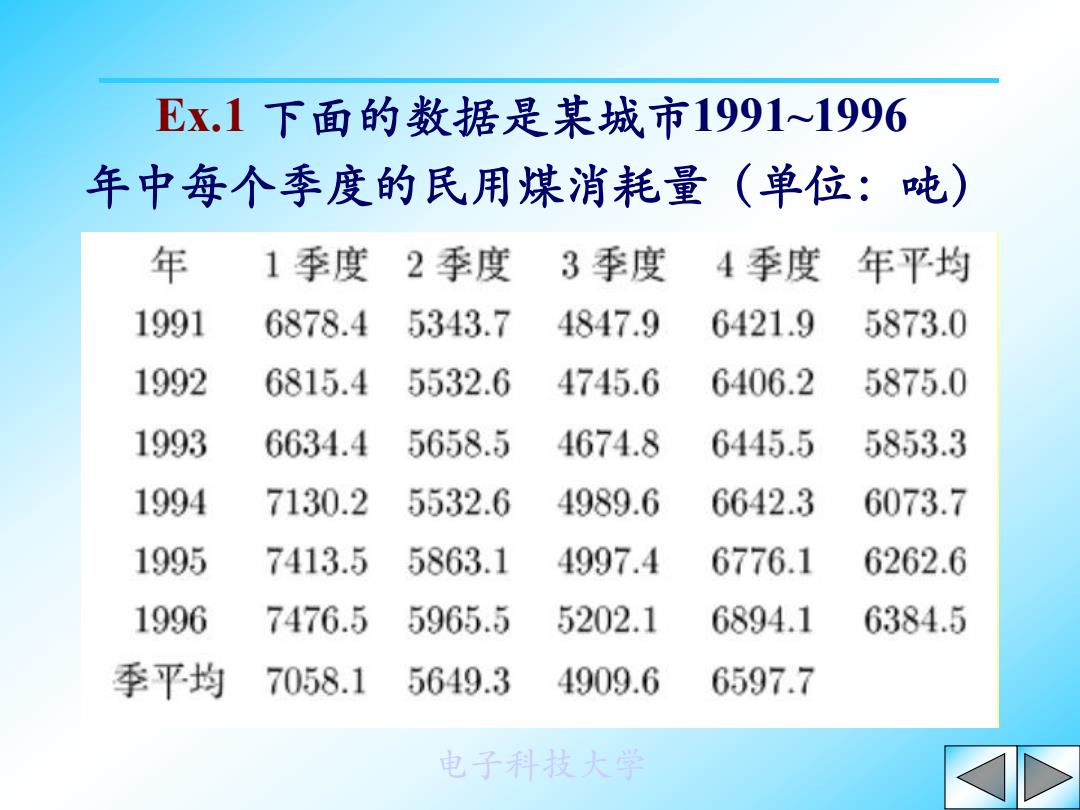
Ex.1下面的数据是某城市1991~1996 年中每个季度的民用煤消耗量(单位:吨) 年 1季度2季度 3季度 4季度 年平均 1991 6878.4 5343.7 4847.9 6421.9 5873.0 1992 6815.4 5532.6 4745.6 6406.2 5875.0 1993 6634.4 5658.5 4674.8 6445.5 5853.3 1994 7130.2 5532.6 4989.6 6642.3 6073.7 1995 7413.5 5863.1 4997.4 6776.1 6262.6 1996 7476.5 5965.5 5202.1 6894.1 6384.5 季平均 7058.1 5649.3 4909.6 6597.7 电子科技大学
电子科技大学 Ex.1 下面的数据是某城市1991~1996 年中每个季度的民用煤消耗量(单位:吨)