电子科技大学：《随机过程及应用 Stochastic Processes and Applications》课程教学资源（课件讲稿）第5章 平稳随机过程 第2节 平稳过程的自相关函数

§5.2平稳过程的自相关函数 平稳过程自相关函数的性质 定理5.2.1 复平稳过程{X(t),t∈T的自相关函 数Px(T),有如下性质： 1) R0)=EX(t)1≥0： 2)Rx()≤Rx(0);(Cx(T)≤Cx(0);) 3)Rx(-)=Rx(; 电子科技大学

电子科技大学 §5.2 平稳过程的自相关函数 一、平稳过程自相关函数的性质 复平稳过程{X(t),t∈T}的自相关函 数RX (τ), 有如下性质： 定理5.2.1 1) (0) [ ( ) ] 0; 2 R  E X t  2) ( ) (0); RX  RX  3) RX ()  RX (); ( ( ) (0);) CX  CX 

4) 非负定性 对Vn≥1，t1,…,tn∈T, 及复数1,23,0n有 ∑a,aRx(t-t)20. 证明 k,j=1 1) Rx(0)=E{X()X()}=EX(t)}≥0： 2)由许瓦兹不等式 Rx()=Rx(t,t+)=E(X()X(+)) s E[X(t)'JEIX(t+)]=R(0); 电子科技大学

电子科技大学 4) 非负定性 1, , , , 对n  t1  tn T 及复数 α1 ,α2 ,…,αn有     n k j j k X k j R t t , 1   ( ) 0. 证明 1) (0) { ( ) ( )} { ( ) } 0; 2 RX  E X t X t  E X t  2）由许瓦兹不等式 2 2 2 R ( )  R (t,t  )  E(X(t)X(t  )) X X [ ( ) ] [ ( ) ] (0); 2 2 2 RX  E X t E X t  

3)Rx(x)=EX(t)X(t+)川=EX(t)X(t+川 =E[X(t+)X(i++(-)=Rx(-); 4) ∑a,aRxt-) k,j=1 =∑a,a,EX4,)X4l k,i=1 aaX(X(X()10 k,i=1 k=1 电子科技大学

电子科技大学 3) R ( )  E[X(t)X(t  )]  E[X(t)X(t  )] X  [ (  ) (  ( ))] ( ); RX E X t X t    n k j j k X k j R t t , 1 4)   ( )    n k j j k j k E X t X t , 1 [   ( ) ( )]    n k j j k j k E X t X t , 1   [ ( ) ( )] [ ( ) ] 0 2 1     n k k k E X t

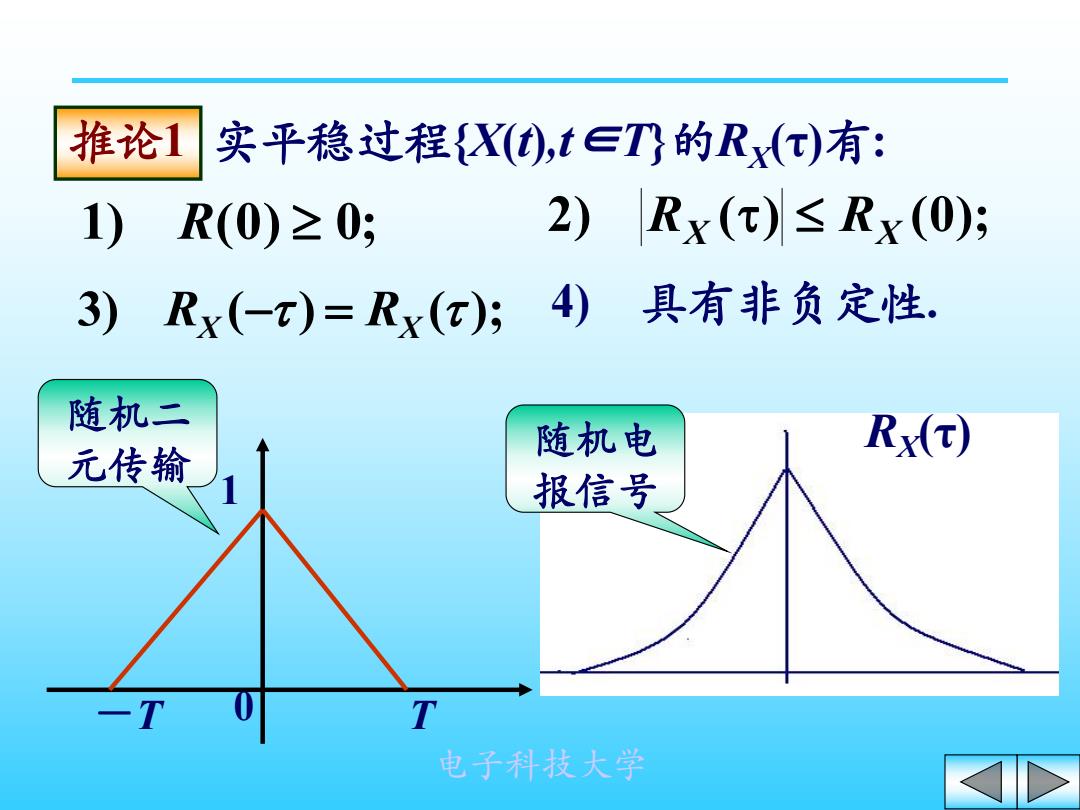
推论1 实平稳过程{X(),t∈T的Rx()有： 1) R(0)≥0； 2)Rx(T)≤Rx(0)； 3)Rx(-T)=Rx(); 4)具有非负定性. 随机二 随机电 Rx(T) 元传输 报信号 T 电子科技大学

电子科技大学 实平稳过程{X(t),t∈T}的RX 推论1 (τ)有: 1) R(0)  0; 2) ( ) (0); RX  RX  3) (  ) ( ); RX   RX 4) 具有非负定性. －T 0 T 1 随机二 RX(τ) 元传输 随机电 报信号

Ex.1讨论随机过程{X(t),仑0}是否为平稳 过程，其中X(t)=sinot,,o在[0,2π]上服从均 匀分布. 解R(S,t)=EX(S)X(t) 60sinosinodo 1「sin2π(t-s) sin2π(t+s) 4元 t-s t+s R(S,)不是关于S-t的偶函数，故实随机过程 X(t),0}不是平稳过程. 电子科技大学

电子科技大学 Ex.1 讨论随机过程{X(t ), t≥0}是否为平稳 过程，其中X(t)=sinωt, ω在[0, 2π]上服从均 匀分布. 解 R(s,t)=E(X(s)X(t))        2 0 2 1 sin s sin td                t s t s t s sin 2 (t s) sin 2 ( ) 4 1 R(s,t)不是关于s−t 的偶函数, 故实随机过程 {X( t ),t≥0}不是平稳过程