定积分的几何意义是曲边梯形的面积y=f(x)A=f'f(x)dx
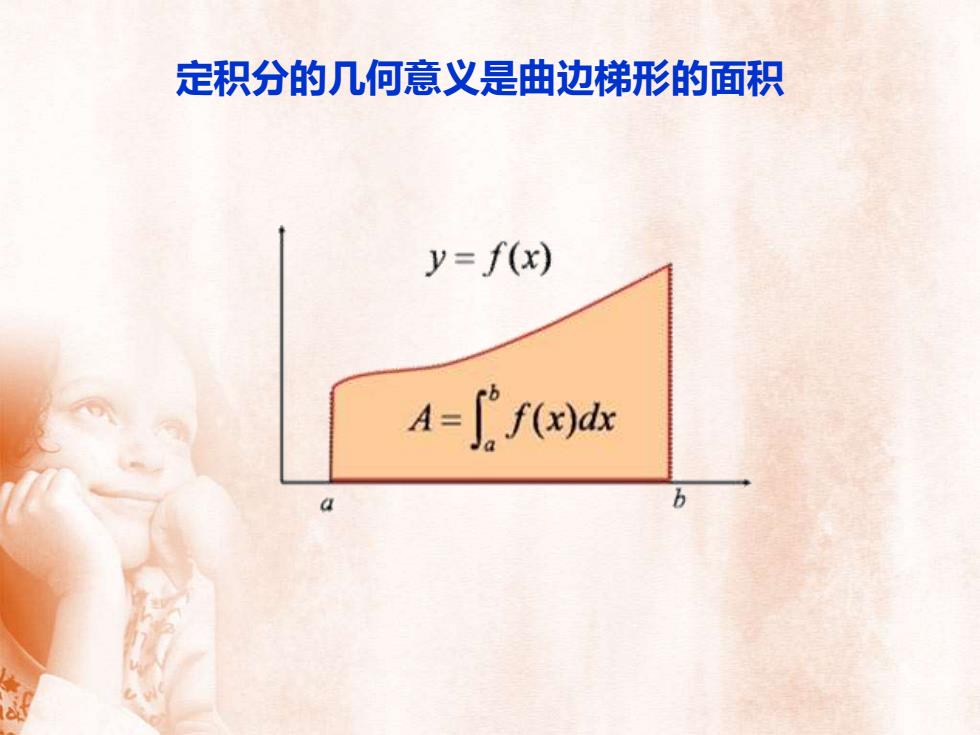
定积分的几何意义是曲边梯形的面积
一、引例1.曲顶柱体的体积柱体体积=底面积×高特点:平顶z= f(x,y柱体体积=?特点:曲顶曲顶柱体
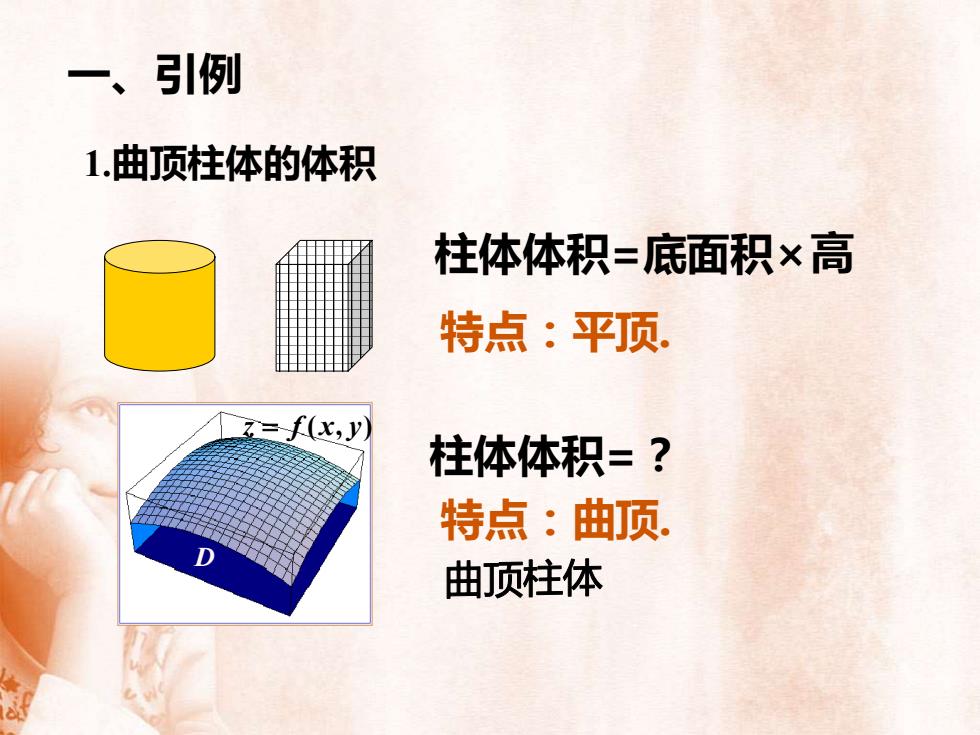
柱体体积=底面积×高 特点:平顶. z = f (x, y) D 柱体体积=? 特点:曲顶. 一、引例 1.曲顶柱体的体积
z = f(x,y)给定曲顶柱体底:xoy面上的闭区域 DD顶: 连续曲面 z= f(x,y)≥0侧面:以D的边界为准线,母线平行于z轴的柱面求其体积解法:美类似定积分解决问题的思想“大化小,常代变,近似和,求极限
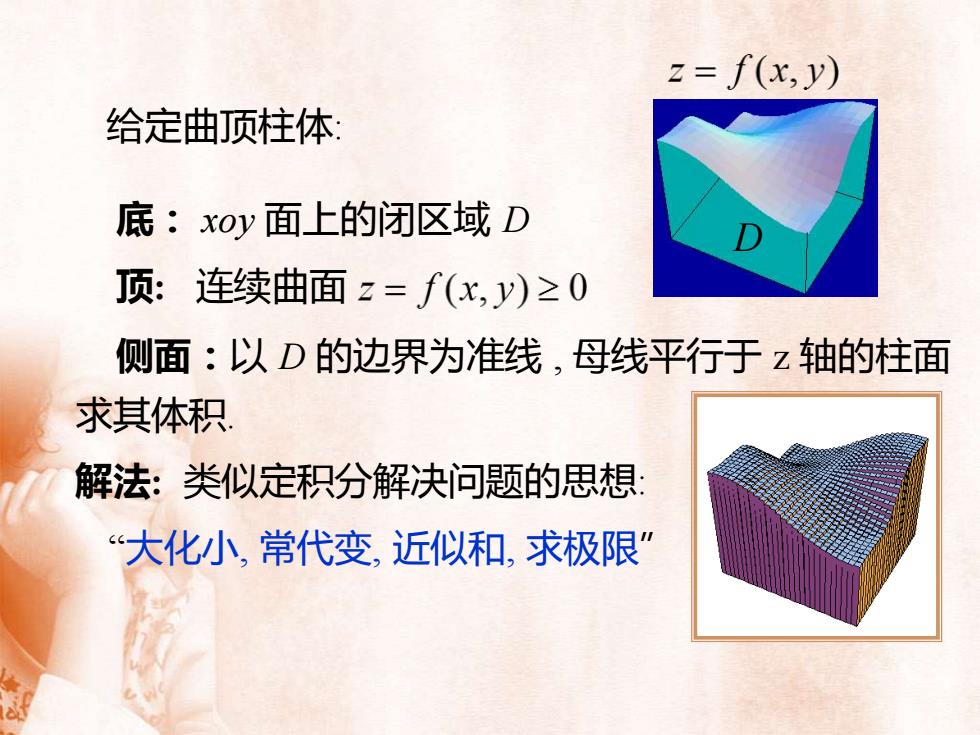
解法: 类似定积分解决问题的思想: 给定曲顶柱体: 底: xoy 面上的闭区域 D 顶: 连续曲面 侧面:以 D 的边界为准线 , 母线平行于 z 轴的柱面 求其体积. “大化小, 常代变, 近似和, 求极限” D
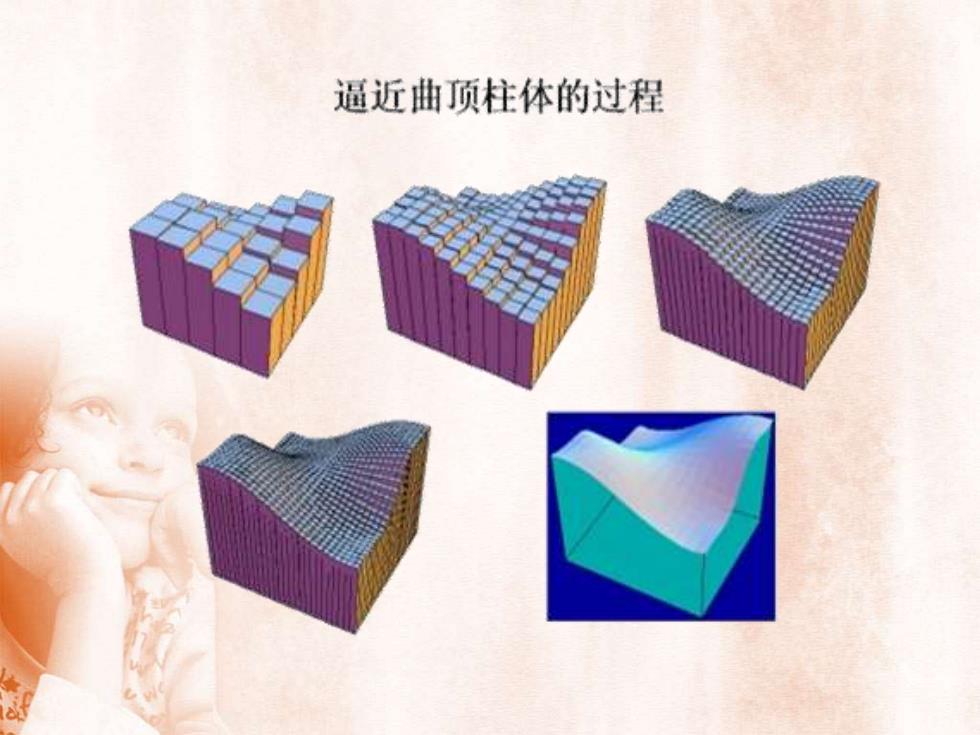
逼近曲顶柱体的过程
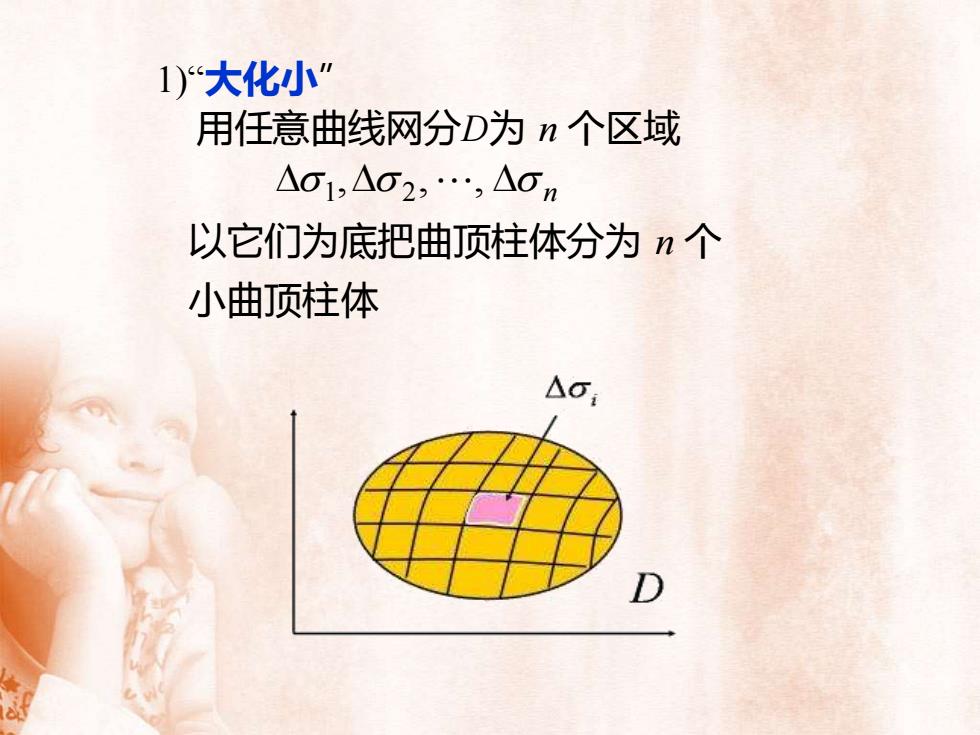
1)“大化小用任意曲线网分D为 n 个区域Ao1,Ao2, ..., Aon以它们为底把曲顶柱体分为 n个小曲顶柱体AoD
1)“大化小” 用任意曲线网分D为 n 个区域 n , , , 1 2 以它们为底把曲顶柱体分为 n 个 小曲顶柱体