导航 课堂·重难突破 探究一一次函数模型 【例1】某地的水电资源丰富, y元 并且得到了较好的开发,电力 充足某供电公司为了鼓励居 110 民用电,采用分段计费的方法 60 来计算电费.月用电量x(单 100 位:kWh)与相应电费y(单位: 200x/kW·h 元)之间的函数关系如图所示
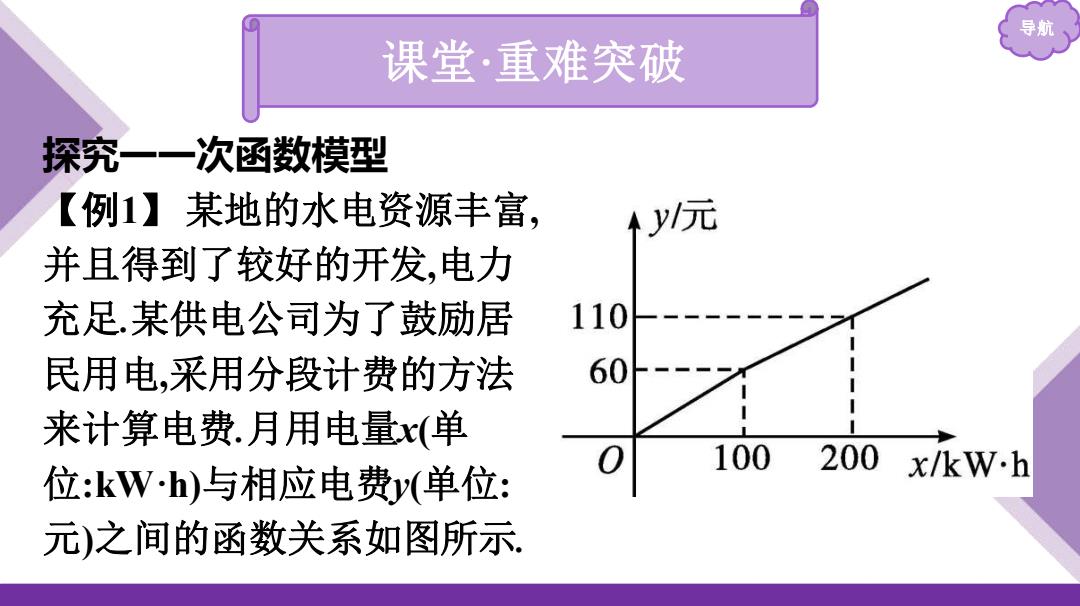
导航 课堂 ·重难突破 探究一一次函数模型 【例 1 】 某地的水电资源丰富 , 并且得到了较好的开发 ,电力 充足 .某供电公司为了鼓励居 民用电 ,采用分段计费的方法 来计算电费 .月用电量x ( 单 位 :kW·h )与相应电费y (单位 : 元 )之间的函数关系如图所示

导航、 (1)当月用电量为100kWh时,应交电费多少元? (2)当x≥100时,求y与x之间的函数解析式; 3)当月用电量为260kWh时,应交电费多少元?
导航 (1)当月用电量为100 kW·h时,应交电费多少元? (2)当x≥100时,求y与x之间的函数解析式; (3)当月用电量为260 kW·h时,应交电费多少元?

导航 解:(1)当月用电量为100kWh时,应交电费60元 (2)当x≥100时y与x之间为一次函数关系. 设广r+b40,则200k+b=110, 100k+b=60, 保号低-数字10 ③)当x=260时y2×260+10=140. 2 故当月用电量为260kWh时,应交电费140元
导航 解:(1)当月用电量为100 kW·h时,应交电费60元. (2)当x≥100时,y与x之间为一次函数关系. 设 y=kx+b(k≠0),则 𝟐𝟎𝟎𝒌 + 𝒃 = 𝟏𝟏𝟎, 𝟏𝟎𝟎𝒌 + 𝒃 = 𝟔𝟎, 解得 𝒌 = 𝟏 𝟐 , 𝒃 = 𝟏𝟎, 故 y= 𝟏 𝟐 x+10. (3)当 x=260 时,y= 𝟏 𝟐 ×260+10=140. 故当月用电量为260 kW·h时,应交电费140元

延伸探究 导 若将本例(2)中的x≥100去掉,其他条件不变,求y与x的函数解 析式 解:因为函数图象不在同一条直线上,所以选择分段求解. 当0≤x≤100时,设y=kx(k0),则60=100k, 解得故 当x>100时,同例1(2),得=之+10 故y= 层x0≤x≤10, 2x+10x>100
导航 若将本例(2)中的x≥100去掉,其他条件不变,求y与x的函数解 析式. 解:因为函数图象不在同一条直线上,所以选择分段求解. 当0≤x≤100时,设y=kx(k≠0),则60=100k, 解得 k=𝟑 𝟓 ,故 y= 𝟑 𝟓 x. 当 x>100 时,同例 1(2),得 y= 𝟏 𝟐 x+10. 故 y= 𝟑 𝟓 𝒙,𝟎 ≤ 𝒙 ≤ 𝟏𝟎𝟎, 𝟏 𝟐 𝒙 + 𝟏𝟎,𝒙 > 𝟏𝟎𝟎

导航 反思感悟一次函数模型的应用层次要求不高,一般情况下按 照“问什么,设什么,列什么”的原则来处理,求解过程也较简单
导航 反思感悟 一次函数模型的应用层次要求不高,一般情况下按 照“问什么,设什么,列什么”的原则来处理,求解过程也较简单