
全程设计 3.2函数与方程、 不等式之间的关系 第2课时 零点的存在性及其近似值的 求法
3.2 函数与方程、不等式之间的关系 第2课时 零点的存在性及其近似值的 求法
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航 课标定位素养阐释 1.理解函数零点存在定理,会判断函数零,点是否存在 2.掌握二分法求函数零点的步骤及原理 3.会用二分法求函数零点的近似值
导航 课标定位素养阐释 1.理解函数零点存在定理,会判断函数零点是否存在. 2.掌握二分法求函数零点的步骤及原理. 3.会用二分法求函数零点的近似值
导航 课前·基础认知 函数零点存在定理 【问题思考】 1.观察下面函数的图象并回答问题: 函数fx)=x2.4x+3的图象如图. (1)函数fx)的零点是什么? 3x 提示:1和3. (2)判断f0f2)与f24)的符号. 提示:.f0)=3f2)=-1,4)=3,0f2)<0,24)<0
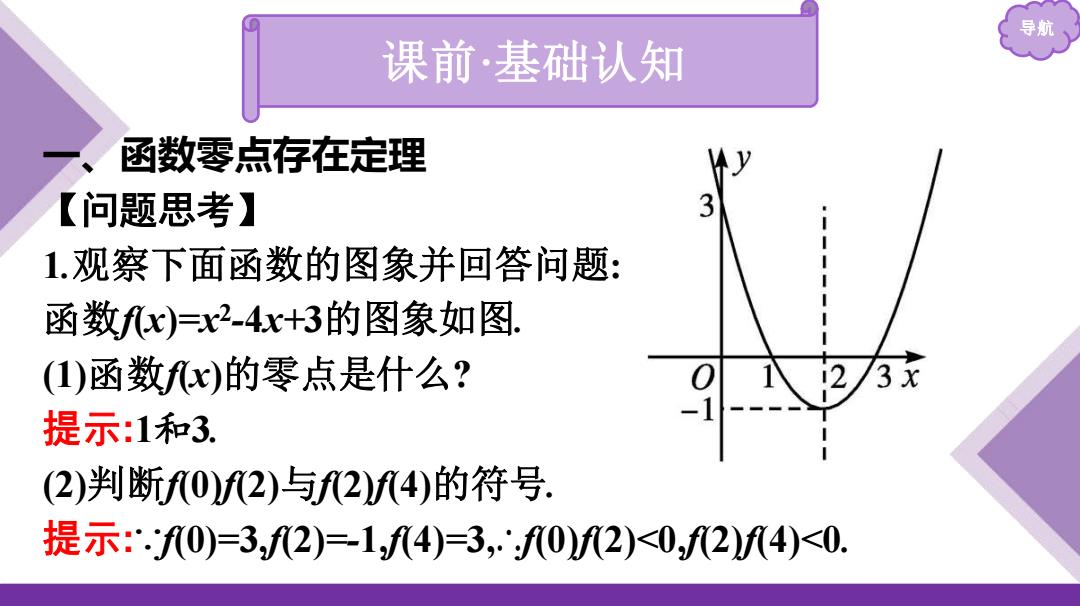
导航 课前·基础认知 一、函数零点存在定理 【问题思考】 1.观察下面函数的图象并回答问题: 函数f(x)=x2 -4x+3的图象如图. (1)函数f(x)的零点是什么? 提示:1和3. (2)判断f(0)f(2)与f(2)f(4)的符号. 提示:∵f(0)=3,f(2)=-1,f(4)=3,∴f(0)f(2)<0,f(2)f(4)<0

导航 2填空: 函数零点存在定理:如果函数y=fx)在区间[,b上的图象是连 续不断的,并且 (即在区间两个端点处的函数值异 号),则函数y=f)在区间(a,b)中至少有一个零点,即x∈(a,b)
导航 2.填空: 函数零点存在定理:如果函数y=f(x)在区间[a,b]上的图象是连 续不断的,并且f(a)f(b)<0 (即在区间两个端点处的函数值异 号),则函数y=f(x)在区间(a,b)中至少有一个零点,即∃x0∈(a,b), f(x0 )=0