
全程设计 3.1.2 函数的单调性 第2课时 函数的最大(小)值
3.1.2 函数的单调性 第2课时 函数的最大(小)值
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练
课标定位素养阐释 课前·基础认知 课堂·重难突破 随堂训练

导航、 课标定位素养阐释 1理解函数的最大(小)值的概念及其几何意义 2.会借助函数的单调性求最值 3.掌握求二次函数在闭区间上的最值
导航 课标定位素养阐释 1.理解函数的最大(小)值的概念及其几何意义. 2.会借助函数的单调性求最值. 3.掌握求二次函数在闭区间上的最值
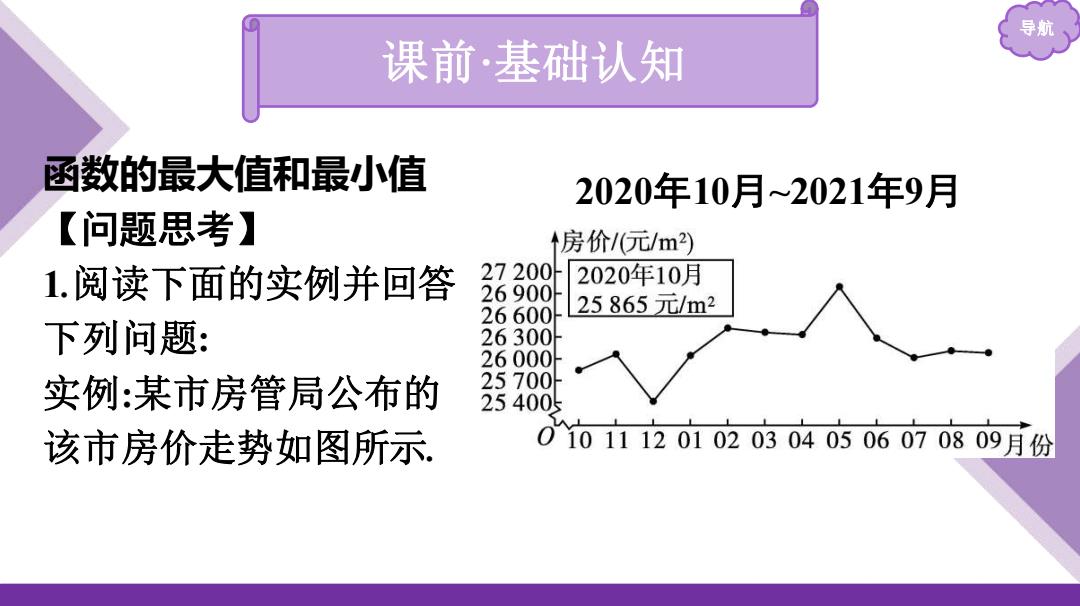
导 课前·基础认知 函数的最大值和最小值 2020年10月~2021年9月 【问题思考】 个房价/元/m2) 1.阅读下面的实例并回答 27200 2020年10月 26900 26600 25865元/m2 下列问题: 26300 26000 实例:某市房管局公布的 25700 254005 该市房价走势如图所示 0101112010203040506070809月份
导航 课前·基础认知 函数的最大值和最小值 【问题思考】 1.阅读下面的实例并回答 下列问题: 实例:某市房管局公布的 该市房价走势如图所示. 2020年10月~2021年9月

(1)从图中能否得出该时期房价的最大值和最小值? 提示:从图中可以看到,该时期房价的最大值为2021年5月份 的价格,为26900元m2,而该时期房价的最小值为2020年12月 份的价格,为25400元m2. (2)从走势图上看,2020年10月房价处于上升期,到2020年11月 开始下降,那么2020年11月的房价是该时期的最大值吗?为什 么? 提示:不是.因为该时期房价的最大值应该是所有房价中的最 大者,很明显2020年11月份的房价不满足这个条件,它只是10 月到12月这个局部时期的最大值
导航 (1)从图中能否得出该时期房价的最大值和最小值? 提示:从图中可以看到,该时期房价的最大值为2021年5月份 的价格,为26 900元/m2 ,而该时期房价的最小值为2020年12月 份的价格,为25 400元/m2 . (2)从走势图上看,2020年10月房价处于上升期,到2020年11月 开始下降,那么2020年11月的房价是该时期的最大值吗?为什 么? 提示:不是.因为该时期房价的最大值应该是所有房价中的最 大者,很明显2020年11月份的房价不满足这个条件,它只是10 月到12月这个局部时期的最大值