
8(-1)"2判断级数是否收敛?n-lnn1=18(-1)n8W由莱布尼茨定理是交错级数,n-lnnn=1(x>0)(1) : f(x)=x-lnxf'(x)=1->0(x >1)x1.在(1,+o)上单增,即单减x-lnx1故当n>1时单减n-lnn11u..:Un+1(n>1)n-lnn(n + 1)- In(n+1)
由莱布尼茨定理 f (x) = x − ln x (x 0) x f x 1 ( ) = 1− 在(1,+ )上单增,即 单减 x ln x 1 − = − − 1 ln ( 1) n n n n 是交错级数, 0 (x 1) 判断级数 是否收敛? = − − 1 ln ( 1) n n n n (1) 1 ( 1) ln( 1) 1 = + + − + un n n n ln n 1 − 故 当 n 1时单减 (n 1) n n un ln 1 − =
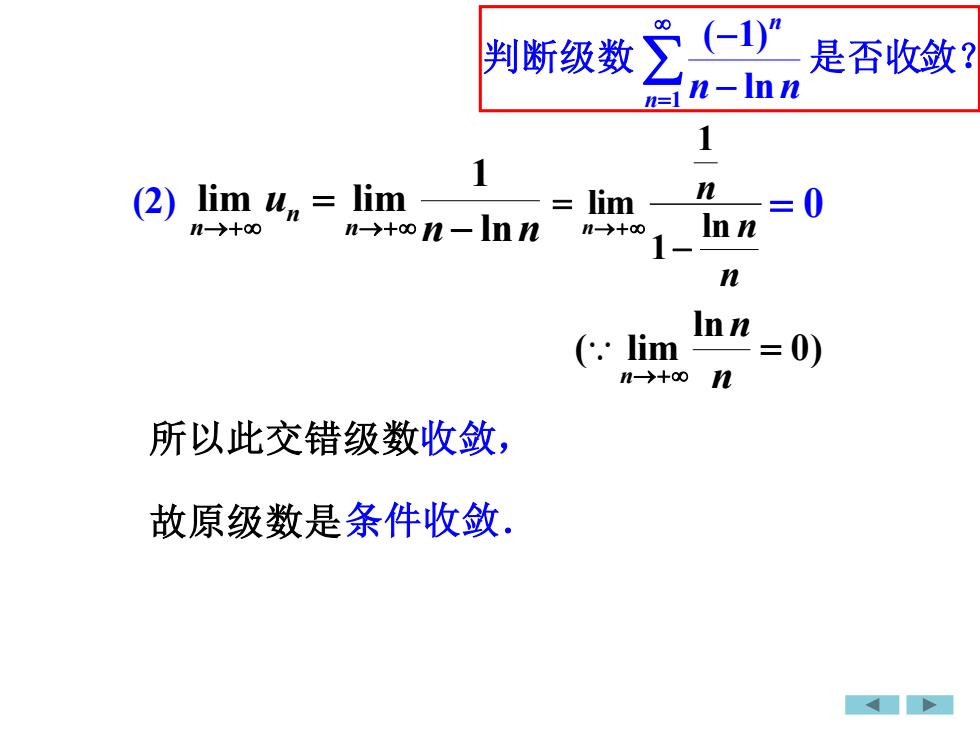
8(-1)"2判断级数是否收敛?n-lnnn=111nlim u. = lim(2)=0limInnn-→+o n- lnnn→+80n→+nInn:0limnn→+0所以此交错级数收敛,故原级数是条件收敛
所以此交错级数收敛, 故原级数是 判断级数 是否收敛? = − − 1 ln ( 1) n n n n 0) ln ( lim = →+ n n n n n u n n n ln 1 lim lim − = →+ →+ n n n n ln 1 1 lim − = →+ (2) = 0 条件收敛.

80Z例求级数(n+1)(x-1)" 收敛域及和函数n=08解E(n+ 1)(x-1)"收敛半径为R=1n=0收敛域为-1<x-1<1,即0<x<2设此级数的和函数为s(x),则有8s(x)= (n+1)(x-1)"两边逐项积分中n=08ZJ (n+1)(x-1)"dxs(x)dx =n=00Z(x-1)*+| =(x-1)+n=0n=0
( 1)( 1) . 0 求级数 收敛域及和函数 = + − n n 例 n x 解 = + − 0 ( 1)( 1) n n n x 即0 x 2 = = + − 0 ( ) ( 1)( 1) n n s x n x 两边逐项积分 R = 1 −1 x −1 1, s(x)dx x 1 = + = − 0 1 1 ( 1) n n x x = + = − 0 1 ( 1) n n x 收敛半径为 收敛域为 设此级数的和函数为s(x), 则有 1 0 ( 1)( 1) d x n n n x x = = + −