《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-习题课

二、典型例题例判断级数敛散性nM(1)n=1(n+n1nnnnn解u.分母lim(1XJiml(1n-8nn→80

二、典型例题 例 判断级数敛散性 解 n n n n u ) 1 ( + = n n n n ) 1 (1 2 1 + =  n n n n 1 ; ) 1 ( (1) 1 1   = + + n n n n n n n n n n ) 1 lim(1 2 + →  n n n n 1 2 ) ] 1 lim[(1 2 = + → 1 0 分母 = e =

8nn(1) Zn+nhn后(n+-)nUY(n+=)1+nn分子:limxx =e°=1:. limnn =1x-n->0分母n>00.. limu. =1￥0n→00根据级数收敛的必要条件，级数发散

x x x 1 lim →  1 0 = e = lim = 1 → n n u 根据级数收敛的必要条件，级数 分子 lim 1 1  = → n n n  0 ) 1 1 lim(1 2 + = → n n n  n n n n n n n u ) 1 ( 1 + = + n n n n ) 1 (1 2 1 + = 分母 发散．   = + 1 + 1 ) 1 ( (1) n n n n n n n

8In(n +2)>(2)(a>0)n=(a+=)"n正In(n+ 2)n=lim "/In(n + 2)解limlim三u1nn>00a n->on-→00a+-nlim: lim"/ln(n+2) =1,从而有n->00an→00当α>1 即0<=<1时,级数收敛;a当0<a<1即>1时，级数发散;a

正 解 从而有 当a  1 级数 当0  a  1 级数   =  + + 1 ( 0) ) 1 ( ln( 2) (2) n n a n a n 1 , 1 即0   时 a 1 , 1 即  时 a n n u → lim n n a n n 1 ln( 2) lim + + = → n lim ln( 2) 1 = + → n a n n lim ln( + 2) → n n  n = 1, = → n n lim u n a 1 收敛； 发散;

21(n+2)n=In(n + 2)Z当a=1时,原级数为n=1(1 +=)"nIn(n + 2)lim+8n(1+=)n所以,原级数也发散

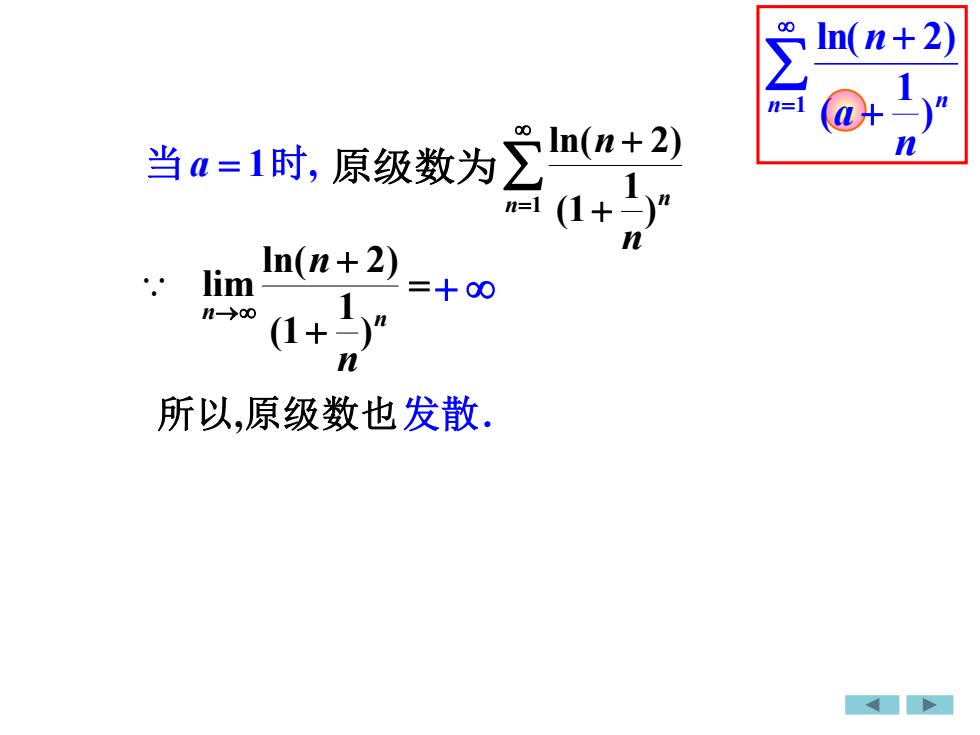
当a = 1时, 原级数为= + + → n n n n ) 1 (1 ln( 2)  lim 所以,原级数也   = + + 1 ) 1 ( ln( 2) n n n a n   = + + 1 ) 1 (1 ln( 2) n n n n +  发散．

:W(-1)n例判断级数是否收敛？如果收敛n=i n- lnn是条件收敛还是绝对收敛？88(-1)"12解 n-lnnn-lnnn=n=]11nn-Innlimlimlim11In nn->0n-lnnn0n>nn808(-1)"1122.而发散二发散,-lnnn-lnnnn=ln=i nn即原级数非绝对收敛

例 解 n n ln n 1 1 lim − = →   =1 1 n n 而   = − − 1 ln ( 1) n n n n 即原级数    =  = − = − − 1 1 ln 1 ln ( 1) n n n n n n n n n n ln 1 lim − →   = − = 1 ln 1 n n n n n n n ln lim − = → = 1 判断级数  是否收敛？  = − − 1 ln ( 1) n n n n 如果收敛, 是条件收敛还是绝对收敛? n 1 发散, 发散 非绝对收敛．