
1 直角坐标系情形 y y=f(x) =f(x) =f(x) o a xx+△bX 0 a b 曲边梯形的面积 曲边梯形的面积 A=[f(x)dx A=心f2(x)-f(x)dc 穿针法或微元素法 被积函数上-下、右-左 2012329 泰山医学院信息工程学院高等数学教研室

例1计算由两条抛物线y2=x和y=x2所围成的 图形的面积, 解两曲线的交点解方程组)=x y=x =2 (0,0)(1,1) 选x为积分变量x∈I0,川 面积元素dA=(Nx-x2)d A=(x-x')dx= 注被积函数为上-下,上为y=x下为y=x 2012.329 泰山医学院信息工程学院高等数学教研室 12
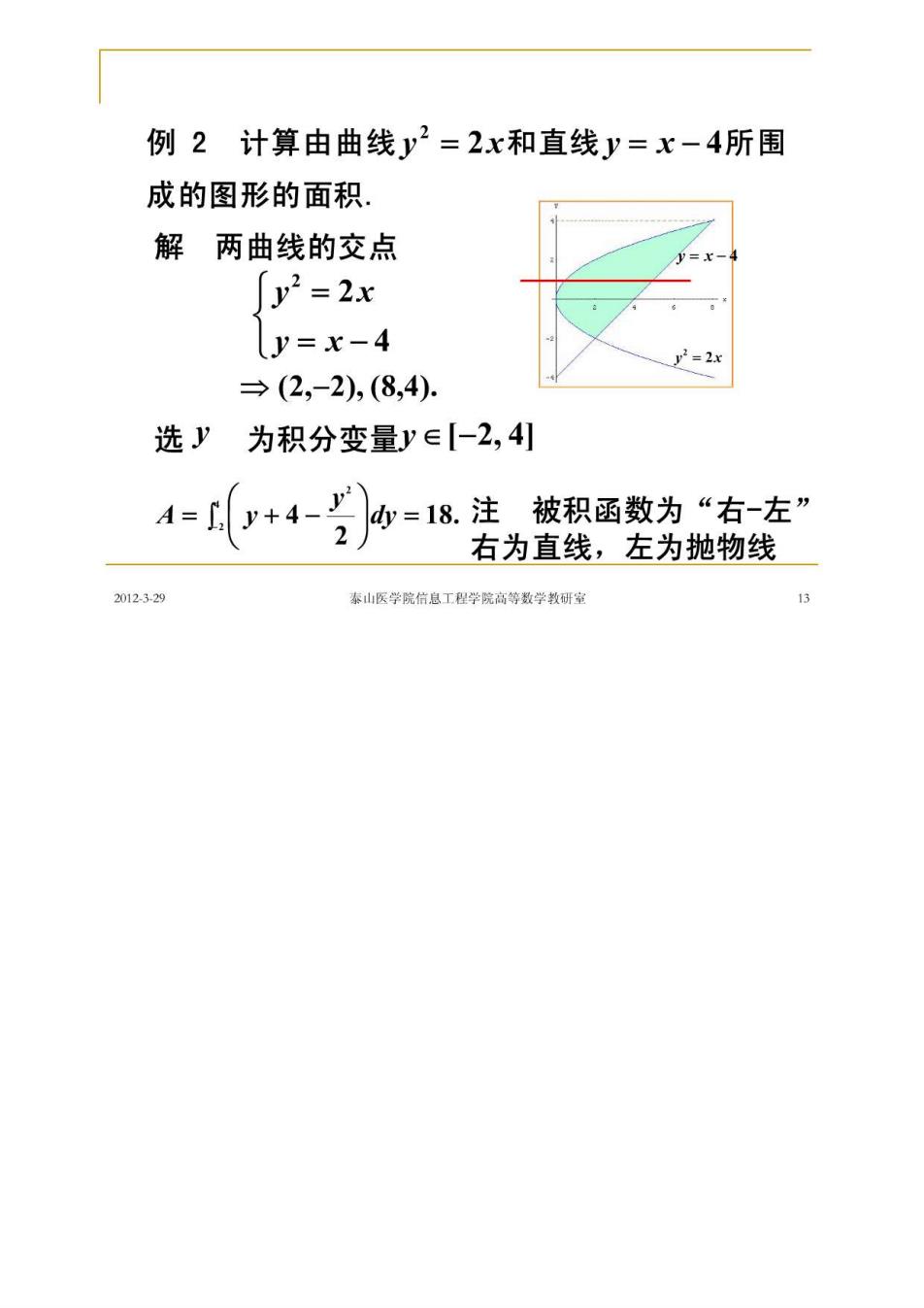
例2计算由曲线y2=2x和直线y=x-4所围 成的图形的面积。 解两曲线的交点 [y2=2x y=x-4 y2=2x →(2,-2),(8,4) 选y 为积分变量y∈【-2,4 4=(+4=收注被积函数为有左” 右为直线,左为抛物线 2012329 泰山医学院信息工程学院高等数学教研室 13

x=0(t) 如果曲边梯形的曲边为参数方程 y=v(t) 曲边梯形的面积 A=y(0o'). (其中1,和t,对应曲线起点与终点的参数值) 在[t,t2](或[t2,t])上x=p(t)具有连续导 数,y=(t)连续. 2012329 泰山医学院信息工程学院高等数学教研室

例3 求椭圆术己 21的面积 x=acost 解 椭圆的参数方程 y=bsint 由对称性知总面积等于4倍第一象限部分面积. A=4 ydx =4bsintd(acost) =4 ab fsini2d=元ah. 2012329 泰山医学院信息工程学院高等数学教研室