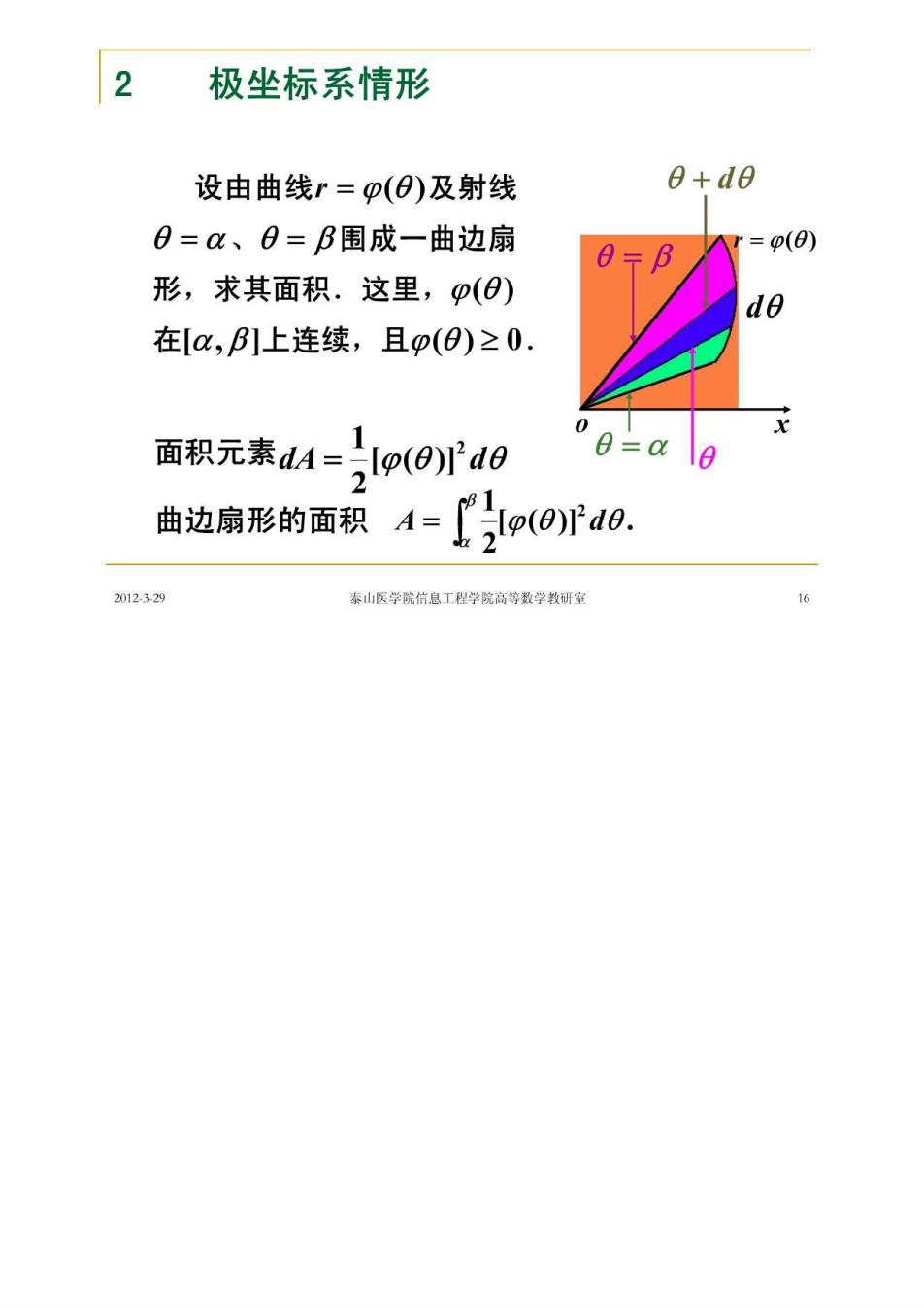
2 极坐标系情形 设由曲线r=p()及射线 0+d0 0=a、0=B围成一曲边扇 0-B r=o(0) 形,求其面积.这里,p() 在a,B1上连续,且p(0)≥0 面积元素A=pod0 曲边扇形的面积A=o(ora0. 2012329 泰山医学院信息工程学院高等数学教研室

例4求阿基米德螺线r=a0(a>0)上相应 于日从0到2π的弧与极轴所围成的图形的面 积. 解.0∈I0,2π] 1 dA=-(a202)d0 2 于是 36 24 12 3z 2012329 泰山医学院信息工程学院高等数学教研室

例5求心形线r=a(1+c0s)所围平面图形 的面积(a>0). 解dAe+cosa2d6 利用对称性知 1-2.(csd0 21 =af(1+2cos0+cos20)d0 +2sin+ a3 7π3 sin 20 4 2012329 泰山医学院信息工程学院高等数学教研蜜

例4求双纽线p2=a2c0s20所围平面图形 的面积 解由对称性知总面积=4倍第 一象限部分面积 Y=x A=4A1 =4G,a2cos28/0=a 2012329 奉山医学院信息工程学院高等数学教研室