《复变函数与积分变换》课程教学资源（PPT课件）第一章 复数与复变函数 1.3 第三节 复数的乘幂与方根

复变函数两个复数的商的模等于它们的模的商：两定理二个复数的商的辐角等于被除数与除数的辐角之差按照商的定义，当21#0时，z2=孕Z1,证Z17212Argz2 = Arg+ Argz1'Z72Z1Z1Z172Z2N于是Arg= Argz2 - Argz1Z1KZ1设复数z,和z,的指数形式分别为Z1 =rieio,，Z2 = rei0,, 则2= ei(2,-2),i0,[证毕]Z1riU

6 定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差. 证 按照商的定义, 0 , 当z1  时 , 1 1 2 2 z z z z = , 1 1 2 2 z z z z = Arg Arg Arg , 1 1 2 2 z z z z  +      = , 1 2 1 2 z z z z 于是 = Arg Arg Arg . 2 1 1 2 z z z z  = −      设复数z1和z2的指数形式分别为 , 1 1 1 i z = r e . ( ) 1 2 1 2  2−1 = i e r r z z z2 = r2 e i 2 , 则 [证毕]

复变函数元元(1- ~/3i),例1 已知icos， Zz = sinZ1二33求Z: 和Z.2元-3元-3解因为 z = cos+isinRC元+isinZ2 = cOS6)元元元元=-i,所以 z1: Z2 = COS+isin3636V3元元元元Z1+isin=cos一332266Z2U

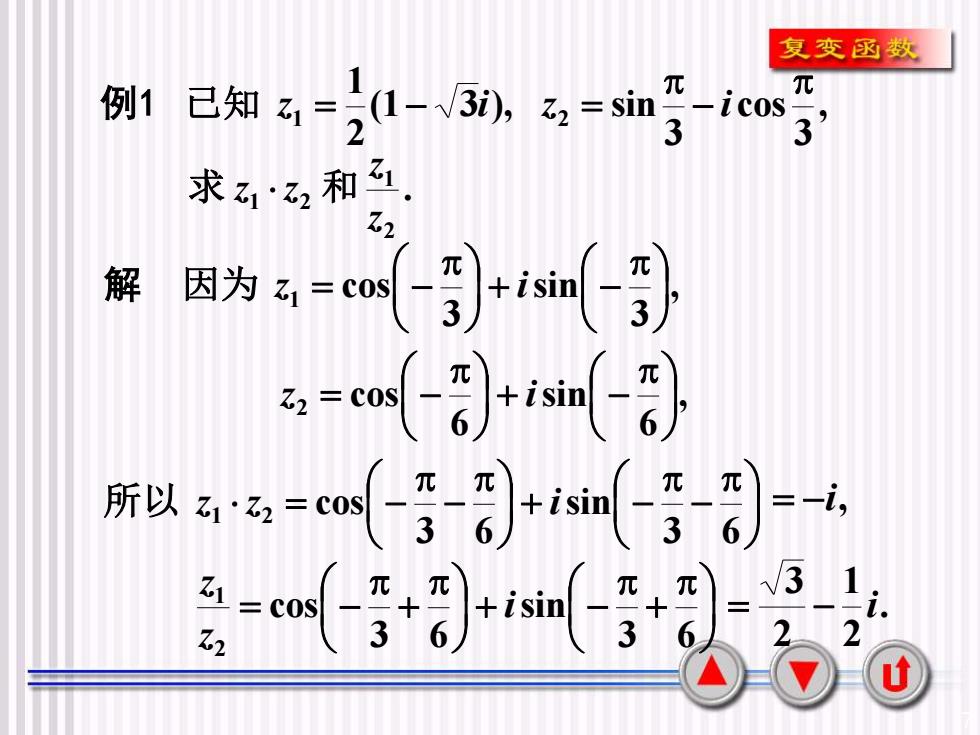
7 例 1 解 , 3 cos 3 (1 3 ), sin 21 1 2  −  已知 z = − i z = i , 3 sin 3 cos 1     + −    因为 z = − i , 6 sin 6 cos 2     + −    z = − i    −   + −    −   = − 3 6 sin 3 6 cos 1 2 所以 z z i = − i ,    +   + −    +  = − 3 6 sin 3 6 cos 21 i zz . 21 23 = − i . 21 1 2 zz 求 z z 和

复变函数例2 已知正三角形的两个顶点为z =1和z2=2+i求它的另一个顶点13解如图所示,Z2 =2 +i元-3将表示 z2 -z的向量+x=1ZZ3绕旋转(或-)就得33到另一个向量,它的终点即为所求顶点 (或)元元-3因为复数e3 的模为1,转角为u

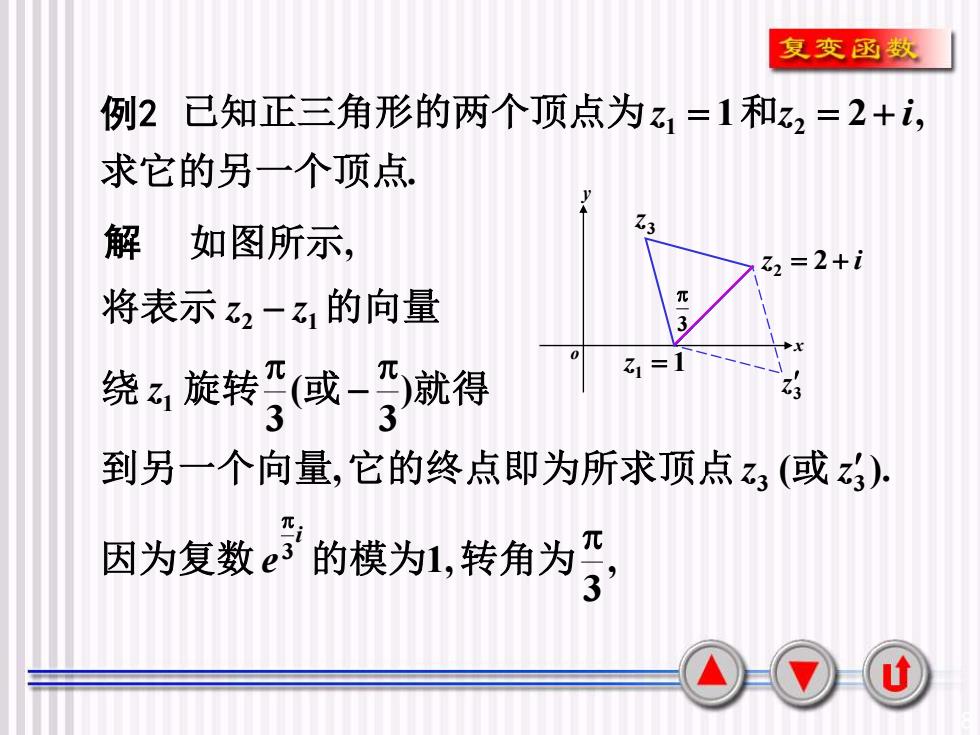
8 例2 解 . 1 2 , 1 2 求它的另一个顶点 已知正三角形的两个顶点为z = 和z = + i , ( ). ) 3 ( 3 3 3 1 2 1 z z z z z   −  − 到另一个向量 它的终点即为所求顶点 或 绕 旋转 或 就得 将表示 的向量 如图所示, o x y z1 = 1 z = 2 + i 2 3 z 3 z  3  , 3 1, 3   因为复数 的模为 转角为 i e

复变函数元i1=e3(Z2 - Zl)Z3 - Z1y+15311小+(1 +i)22Z2 = 2+i元-3(6-9)(+)+x0=1Z1Z31+~33-V33+/3/3LIV所以 z3 1.Z3十1/2222U

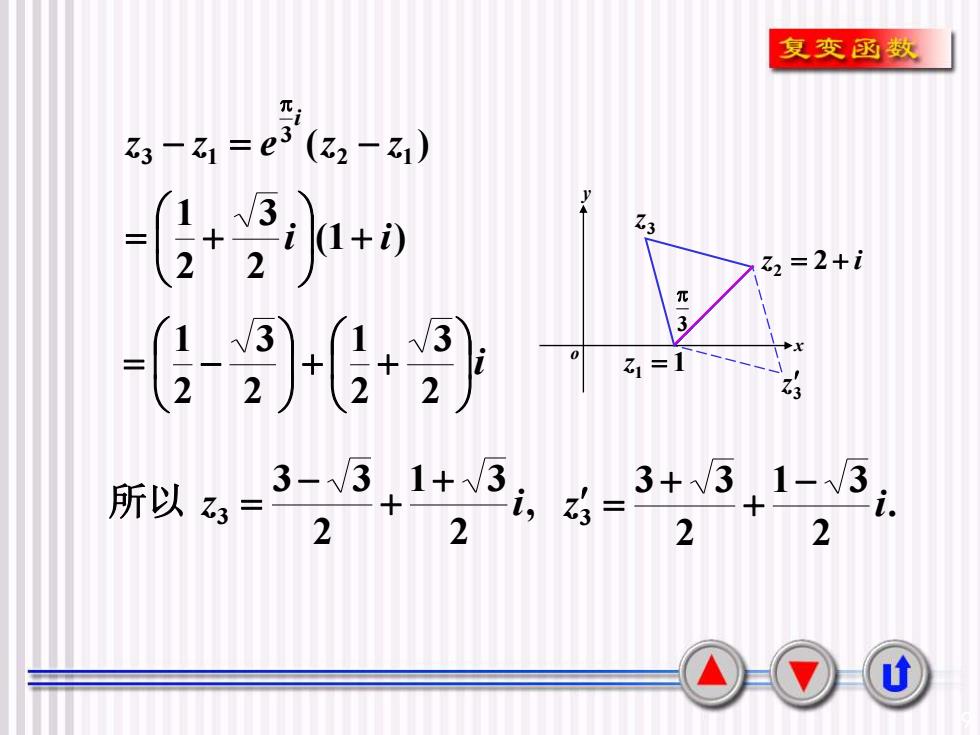
9 ( ) 2 1 3 3 1 z z e z z i − = −  o x y z1 = 1 z = 2 + i 2 3 z 3 z  3  (1 ) 2 3 2 1 i + i      = + i       + +      = − 2 3 2 1 2 3 2 1 , 2 1 3 2 3 3 3 z i + + − 所以 = . 2 1 3 2 3 3 3 z i − + +  =