三、二次插值 已知 0 x X2 % 方 y2 要求构造一个不超过二次的代数多项式 B(x)=ax2+ax +ao 使满足 (x)=f(x,)=y,i=0,1,2 不妨令 B(x)=A(x-x)(x-x)+B(x-x)(x-x2)+C(x-x)(x-x)
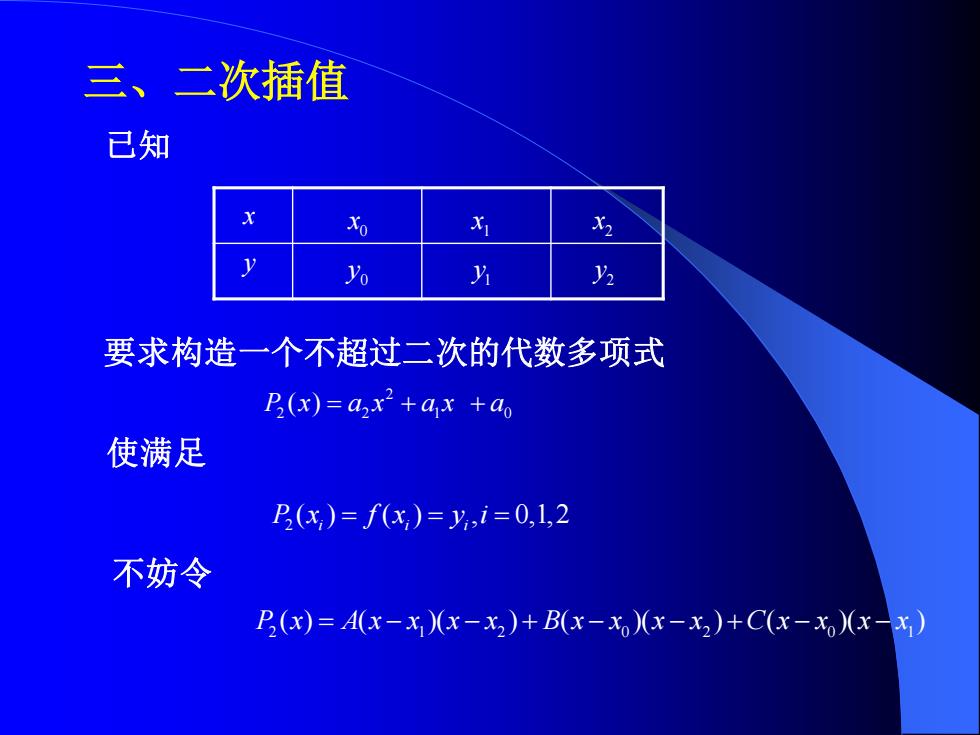
三、二次插值 已知 x y 0 x 1 x 2 x 0 y 1 y 2 y 要求构造一个不超过二次的代数多项式 2 2 2 1 0 P x a x a x a ( ) = + + 使满足 2 ( ) ( ) , 0,1,2 P x f x y i i i i = = = 不妨令 2 1 2 0 2 0 1 P x A x x x x B x x x x C x x x x ( ) ( )( ) ( )( ) ( )( ) = − − + − − + − −

由条件(x,)= 0=01,2),得 A=%(x。-x)(x。-x2) B=/x)(x2) C=y2/(x2-xo)(x2-x) 于是得到二次插值(或抛物插值)函数 -2- ),(x-x)x-x2 (G-x3-)+ x-x)x-x2) ,(x-x)(x-x)》 (32-x)(2-x) (1.3) 若记 1) (x-x)x-x2) (x-x)(x0-x2) 4(x)= (x-x)(x-x2) 12(x)= (x-x)(x-x) x-x)(x-x) (x2-x)(x2-x)
由条件 2 ( ) ( 0,1,2) P x y i i i = = , 得 0 0 1 0 2 1 1 0 1 2 2 2 0 2 1 /( )( ) /( )( ) /( )( ) A y x x x x B y x x x x C y x x x x = − − = − − = − − 于是得到二次插值(或抛物插值)函数 ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) ( )( ) 1 2 0 2 2 0 1 0 1 0 2 1 0 1 2 0 2 2 2 0 2 1 ( ) x x x x x x x x P x y y x x x x x x x x x x x x y x x x x − − − − = + − − − − − − + − − (1.3) ( )( ) ( )( ) 1 2 0 0 1 0 2 ( ) x x x x l x x x x x − − = − − ( )( ) ( )( ) 0 2 1 1 0 1 2 ( ) x x x x l x x x x x − − = − − ( )( ) ( )( ) 0 1 2 2 0 2 1 ( ) x x x x l x x x x x − − = − − 若记

或统一写成7,()=-j=0,12 则(1.3)成为 Bx)=,x)+4()+4()=∑x) 此式成为抛物插值的Lagrange形式。其中,(x)具有如下性质: 8- i≠》 i,j=0,12
或统一写成 2 0 ( ) , 0,1,2 i j i j i i j x x l x j = x x − = = − 则(1.3)成为 2 2 0 0 1 1 2 2 0 2 2 0 0 ( ) ( ) ( ) ( ) ( ) ( ) j j j i j j i j i i j P x y l x y l x y l x y l x x x y x x = = = = + + = − = − 此式成为抛物插值的 Lagrange 形式。其中 ( ) j l x 具有如下性质: 1, ( ) 0, j i ij i j l x i j = = = i j , 0,1,2 =