
例7计算 31-1 D -5 3 -4 o 1 -1 1 3 -3 解 1 3 -1 3-1 3 Df1-c 1 -5 3 -4 n-n -8 -6 0 2 1 -1 0 2 -1 -5 1 3 -3 16 -2 1 3 -1 2 11 3 -1 2 “0 2 1 -1 r+4r 1 -1 -8 4 -6 r4-8n 0 0 8 -10 016-2 1) 00-10 15 113-1 +n02 1 -1 00 8 -10=40. 000 上述解法中,先用了运算c,c2,其目的是把a,换成I,从而利用运算r,- a1r1,即可把a1(i=2,3,4)变为0.如果不先作c1一c2,则由于原式中a1=3, 需用运算,-把an变为0,这样计算时就比较麻烦.第二步把r2-”1和 r4+5r,写在一起,这是两次运算,并把第一次运算结果的书写省略了. 例8计算 |3111 D 1311 1131 1113 解这个行列式的特点是各列4个数之和都是6.今把第2,3,4行同时加 到第1行,提出公因子6,然后各行减去第一行: 6666 1111 Dtntn31166311 1131 1131 1113 1113 ·12·

|1111川 ra-F 0200 r4-100020 =48. 0002 例9计算 a b d aa+b a+b+c a+b+c+d D= a 2a+b 3a+2b+c 4a+3b+2c+d a 3a+b 6a+3b+c 10a+66+3c+d 解从第4行开始,后行减前行, a b d ra-ra D 0 aa+b a+b+c r2-ri 0 a 2a+b 3a+26+c 0 a 3a+b 6a+3b+cl a b c d n-r 0 a atb a+b+c r3-r:00 a 2a+b 00 a 3a+b a b c d rs-r3 0 aa+b a+b+c 0.0a =a. 2a+b 00 0 a 上述诸例中都用到把几个运算写在一起的省略写法,这里要注意各个运算 的次序一般不能颠倒,这是由于后一次运算是作用在前一次运算结果上的缘故 例如 a b ntr atc b+d nn atc b+d c d c d -a-6 a b ri-r a bntra c d c d c-a d-b lc-a d-b 可见两次运算当次序不同时所得结果不同.忽视后一次运算是作用在前 次运算的结果上,就会出错,例如 a b ntr a+c b+d c d r-n c-a d-b 这样的运算是错误的,出错的原因在于第二次运算找错了对象. 此外还要注意运算r,+与r,+,的区别,记号r,+kr,不能写作r+ ·13

(这里不能套用加法的交换律). 上述诸例都是利用运算”,+k把行列式化为上三角形行列式,用归纳法 不难证明(这里不证)任何n阶行列式总能利用运算,+如,化为上三角形行列 式,或化为下三角形行列式(这时要先把a1,.,a-1化为0).类似地,利用列 运算c,+c,也可把行列式化为上三角形行列式或下三角形行列式. 例10设 au.at 0 D= cl.cb.b. c.cdb.bn al.a D,=det(ag)=: a.au b1.b1. D2=det(b)=:: bnl.bnn 证明D=D,D2 证对D,作运算r,+A,把D,化为下三角形行列式,设为 0 D= =p1.pu, P.p 对D2作运算c,+AG,把D2化为下三角形行列式,设为 91 0/ D2=: =911.gn 于是,对D的前k行作运算r,+Ar,再对后n列作运算c,+Ac,把D化为 下三角形行列式 ·14·
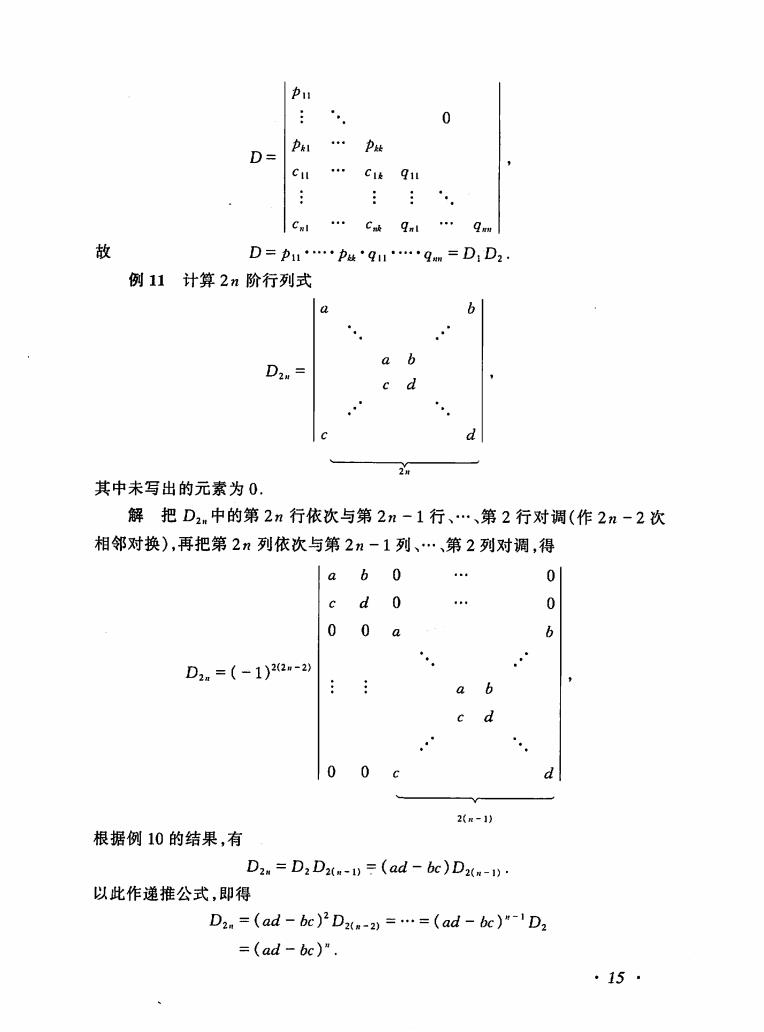
0 D= . 911 D=p1.p41.qm=D1D2 例11计算2n阶行列式 . . d 2 其中未写出的元素为0. 解把D2.中的第2n行依次与第2n-1行、.、第2行对调(作2n-2次 相邻对换),再把第2n列依次与第2n-1列、.、第2列对调,得 ab0. 0 c d 0 0 00a b D2.=(-1)22-2 a 6 0 0 2e-1 根据例10的结果,有 D2.=D2 Di-=(ad-bc)Da-1). 以此作递推公式,即得 D2.=(ad-bc)2D-2n=.=(ad-bc)"-'D2 =(ad-bc)". ·15

§6行列式按行(列)展开 一般说来,低阶行列式的计算比高阶行列式的计算要简便,于是,我们自然 地考虑用低阶行列式来表示高阶行列式的问题.为此,先引进余子式和代数余子 式的概念. 在n阶行列式中,把(i,j)元av所在的第i行和第j列划去后,留下来的 n-1阶行列式叫做(i,j)元a的余子式,记作Mg:记 AG=(-1)Mg, Ag叫做(i,j)元a,的代数余子式 例如四阶行列式 au an ans a D=aa az an au an an asas ast an ass au 中(3,2)元a2的余子式和代数余子式分别为 anan ais Mn=an an azs as ass as A2=(-1)3+2M2=-M2 引理一个n阶行列式,如果其中第i行所有元素除(i,j)元a:外都为零 那么这行列式等于a,与它的代数余子式的乘积,即 D=aA 证先证(i,j)=(1,1)的情形,此时 al0.0 D= a21a2.a2. axla2.an 这是例10中当k=1时的特殊情形,按例10的结论,即有 D=aurMu, 又 A1=(-1)'M,=M1, 从而 D=aA. 再证一般情形,此时 ·16·