
全程设计 第四章 指数函数、对数函数与幂函数 4.1.2 指数函数的性质与图象 第2课时 指数函数及其性质的应用
第四章 指数函数、对数函数与幂函数 4.1.2 指数函数的性质与图象 第2课时 指数函数及其性质的应用

课前·基础认知 课堂·重难突破
课前·基础认知 课堂·重难突破
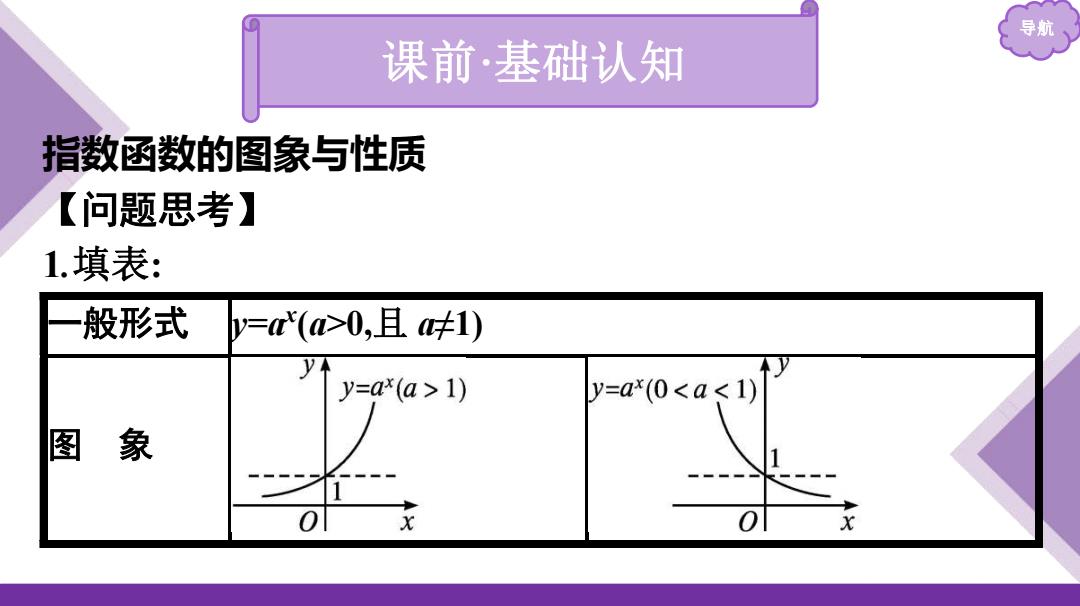
导航 课前·基础认知 指数函数的图象与性质 【问题思考】 1.填表: 般形式 y='(>0,且味1) y y=a*(a>1) y=ax(0<a<1) 图 象 1 0 x 0 X
导航 课前 ·基础认知 指数函数 的图象 与性质 【问题思考】 1 .填表 : 一般形式 y=ax(a>0, 且 a ≠1) 图 象

定义域 R 值域 过定点 在区间(o0,+0)内是 单调性 在区间(-oo,+o0)内是函数 函数 函数值变 若x>0,则y=>1; 若x>0,则0<y=<1;若x<0, 化情况 若x<0,则0y=<1 则y=>1 补充性质 在y轴右侧时,底数越大,图象越靠上
导航 定义域 R 值 域 (0,+∞) 过定点 (0,1) 单调性 在区间(-∞,+∞)内是 增函数 在区间(-∞,+∞)内是减函数 函数值变 化情况 若 x>0,则 y=ax >1; 若 x<0,则 0<y=ax <1 若 x>0,则 0<y=ax <1;若 x<0, 则 y=ax >1 补充性质 在 y 轴右侧时,底数越大,图象越靠上

导航 2.做一做:(1)若函数fx)=(>0,且呋1)在区间1,3引上是减函 数,则实数a的取值范围是 (2)比较大小:0.20.3 0.29. 答案:1)0,1)(2)≥
导航 2.做一做:(1)若函数f(x)=ax (a>0,且a≠1)在区间[1,3]上是减函 数,则实数a的取值范围是 . (2)比较大小:0.2 0.3 0.2 9 . 答案:(1)(0,1) (2)>