
导航 课堂·重难突破 探究一比较两个数的大小 【例1】比较下列各组数的大小: -1.8 -2.5 (1.525和1.532,(2()和(); 31.72和092(④③)5和() -0.5 0.5 分析:根据函数的单调性比较大小,或结合函数图象比较大小, 或借助中间量比较大小
导航 课堂·重难突破 探究一 比较两个数的大小 【例1】比较下列各组数的大小: (1)1.5 2.5 和 1.5 3.2 ; (2) 𝟓 𝟕 -𝟏.𝟖 和 𝟓 𝟕 -𝟐.𝟓 ; (3)1.7 0.2 和 0.9 2.1 ; (4) 𝟐 𝟑 -𝟎.𝟓 和 𝟑 𝟒 -𝟎.𝟓 . 分析:根据函数的单调性比较大小,或结合函数图象比较大小, 或借助中间量比较大小

解:(1)1.52.5,1.53.2可看做函数y=1.5x的两个函数值,因为底数 1.5>1,所以函数y=1.5r在R上是增函数,因为2.5<3.2,所以 1.52.5<1.53.2 (2)因为0<<1,所以函数=() 在定义域内单调递减,又-1.8>2.5, 所以)<() -1.8 2.5 3)由指数函数性质,得1.70.2>1.7=1,0.92.1<0.90=1, 故1.70.2>0.92.1
导航 解:(1)1.5 2.5 ,1.5 3.2可看做函数y=1.5 x的两个函数值,因为底数 1.5>1,所以函数y=1.5 x在R上是增函数,因为2.5<3.2,所以 1.5 2.5<1.5 3.2 . (2)因为 0< 𝟓 𝟕 <1,所以函数 y= 𝟓 𝟕 𝒙 在定义域内单调递减,又-1.8>-2.5, 所以 𝟓 𝟕 -𝟏.𝟖 < 𝟓 𝟕 -𝟐.𝟓 . (3)由指数函数性质,得1.7 0.2>1.7 0=1,0.9 2.1<0.9 0=1, 故1.7 0.2>0.9 2.1
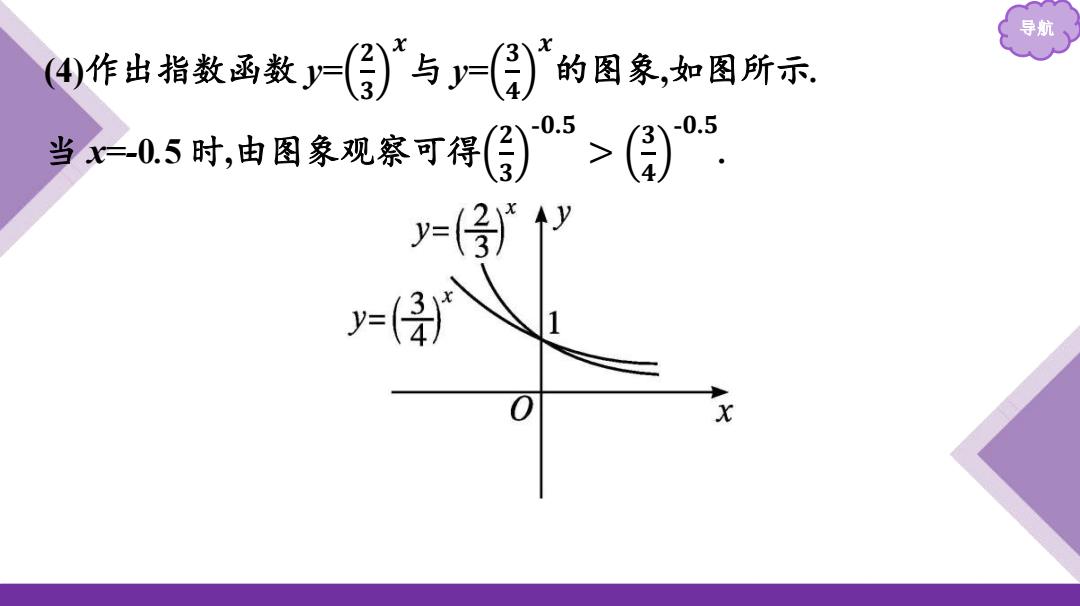
导航 ④作出指数函数()与()的图象,如图所示 当一0.5时,由图象现察可得⑤)05>(图) -0.5 0.5 y=(》y ( 0 X
导航 (4)作出指数函数 y= 𝟐 𝟑 𝒙 与 y= 𝟑 𝟒 𝒙 的图象,如图所示. 当 x=-0.5 时,由图象观察可得 𝟐 𝟑 -𝟎.𝟓 > 𝟑 𝟒 -𝟎.𝟓

导航 了延伸探究 已知a>0,且a1,试比较am2-2m+2与2的大小 解:.'m2-2m+2=(m-1)2+1≥1>-2, .当心1时,am2-2m+2>2; 当0<a<1时,am2-2m+2<r2
导航 已知 a>0,且 a≠1,试比较𝒂 𝒎𝟐 -𝟐𝒎+𝟐 与 a -2 的大小. 解:∵m2 -2m+2=(m-1)2 +1≥1>-2, ∴当 a>1 时,𝒂 𝒎𝟐 -𝟐𝒎+𝟐 >a-2 ; 当 0<a<1 时,𝒂 𝒎𝟐 -𝟐𝒎+𝟐 <a-2