
全程设计 第2课时 两角和与差的正切
第2课时 两角和与差的正切

导航 课标定位素养阐释 1.能推导出两角和与差的正切公式 2.掌握两角和与差的正切公式及变形 3.能利用公式进行简单的求值、化简等. 4.加强逻辑推理能力和数学运算能力的培养
导航 课标定位 素养阐释 1.能推导出两角和与差的正切公式. 2.掌握两角和与差的正切公式及变形. 3.能利用公式进行简单的求值、化简等. 4.加强逻辑推理能力和数学运算能力的培养

课前·基础认知 课堂·重难突破 随堂训练 易错辨析
易 错 辨 析 课前·基础认知 课堂·重难突破 随 堂 训 练

导航、 课前·基础认知 两角和与差的正切 【问题思考】 l.tan(a+f),tan(o-)能否用tana,tanB表示? 提示:能
导航 课前·基础认知 两角和与差的正切 【问题思考】 1.tan(α+β),tan(α-β)能否用tan α,tan β表示? 提示:能
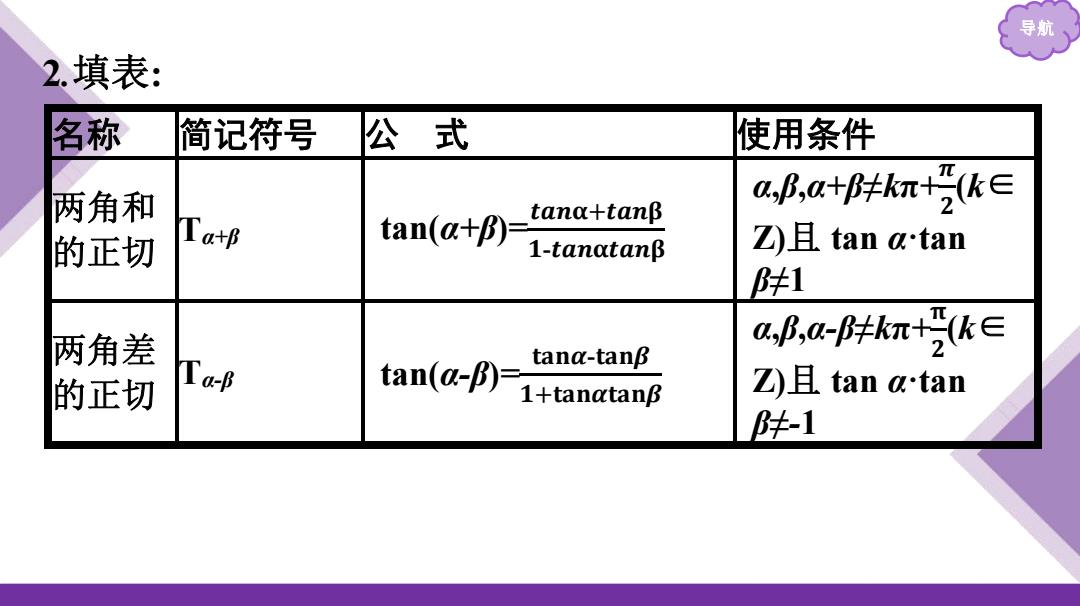
导航 2.填表: 名称 简记符号 公式 使用条件 两角和 a,B,a+p≠kπ+,k∈ tana+tanβ 的正切 TarB tan(a+B)- 1-tanatanβ Z☑且tan a'tan 件1 两角差 a,,-件kT+k∈ 的正切 Ta-B tan(a-B)= tana-tanB +tanatanβ Z且tan a'tan ≠-1
导航 2 .填表: 名称 简记符号 公 式 使用条件 两角和 的正切 T α +β tan( α +β)=𝒕𝒂 𝒏 𝛂 +𝒕𝒂 𝒏 𝛃 𝟏-𝒕𝒂 𝒏 𝛂𝒕𝒂 𝒏 𝛃 α,β,α +β≠ kπ +𝝅𝟐(k ∈ Z)且 tan α·tan β≠1 两角差 的正切 T α-β tan( α-β)= 𝐭𝐚 𝐧 𝜶-𝐭𝐚 𝐧 𝜷 𝟏 +𝐭𝐚 𝐧 𝜶𝐭𝐚 𝐧 𝜷 α,β,α-β≠ kπ +𝛑𝟐(k ∈ Z)且 tan α·tan β≠-1